
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
【答案】(1)答案见解析(2)A.7;B.0<t≤2时,6-t;t>2时,3t-2.
【解析】试题分析:(1)先将各数表示在数轴上,然后按照数轴上越右的数越大用“<”号连接起来即可;
(2)甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>2时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;
A、当t=3时,根据上面的分析进行计算即可得;
B、分0<t≤2与t>2两种情况进行讨论即可得.
试题解析:(1)如图所示:
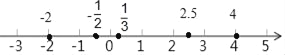
-2<-![]() <
<![]() <2.5<4;
<2.5<4;
(2)∵甲球运动的路程为:1t=t,OA=2,∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,
∵OB=4,乙球运动的路程为:2t=2t,∴乙球到原点的距离为:4-2t;
(Ⅱ)当t>2时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2(t-2)=2t-4;
A、当t=3时,甲、乙两小球之间的距离为:t+2+2t-4=3t-2=7;
B、分两种情况:(Ⅰ)0<t≤2,甲、乙两小球之间的距离为:t+2+4-2t=6-t;
(Ⅱ)t>2,甲、乙两小球之间的距离为:t+2+2t-4=3t-2.


科目:初中数学 来源: 题型:
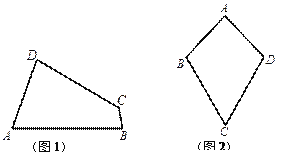
【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形![]() 是“等对角四边形”,
是“等对角四边形”, ![]() ,
, ![]() ,
, ![]() .求
.求![]() ,
, ![]() 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”![]() (如图2),其中
(如图2),其中![]() ,
, ![]() ,此时她发现
,此时她发现![]() 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”![]() 中,
中, ![]() ,
, ![]() ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 6:00 | 4小时 | 264千米 |
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 264千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
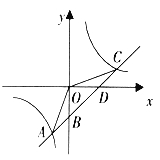
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
(1)求反比例函数![]() 和一次函数
和一次函数![]() 的解析式;
的解析式;
(2)连结OA,OC,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:①AE=CF; ②△EPF一定是等腰直角三角形; ③S四边形AEPF=![]() S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)写出A1,B1,C1的坐标,A1 ;B1 ;C1 .(直接写出答案)
(3)△A1B1C1的面积为 .(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
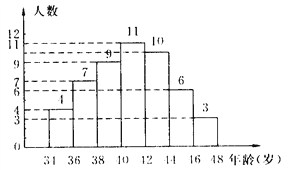
【题目】如图是某单位职工的年龄(取正整数)的频率分布直方图,根据图中提供的信息,回答下列问题:
(1)该单位共有职工多少人?
(2)不小于38岁但小于44岁的职工人数占职工总人数的百分比是多少?
(3)如果42岁的职工有4人,那么年龄在42岁以上的职工有几人?
查看答案和解析>>
科目:初中数学 来源: 题型:
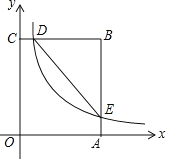
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为3,则k=___________;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com