
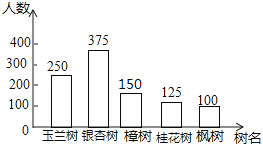
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:
请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为:;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
【答案】
(1)1000
(2)
解:选择“樟树”的有1000﹣250﹣375﹣125﹣100=150(人),
补全条形图如图:
(3)
解:360°× ![]() =36°,
=36°,
答:扇形统计图中“枫树”所在扇形的圆心角度数为36°
(4)
解:8× ![]() =2(万人),
=2(万人),
答:估计这8万人中最喜欢玉兰树的约有2万人
【解析】解:(1)这次参与调查的居民人数有 ![]() =1000(人);
=1000(人);
故答案为:(1)1000.
(1)根据“银杏树”的人数及其百分比可得总人数;(2)将总人数减去选择其它4种树的人数可得“樟树”的人数,补全条形图即可;(3)用样本中“枫树”占总人数的比例乘以360°可得;(4)用样本中最喜欢“玉兰树”的比例乘以总人数可得.本题主要考查了条形统计图,扇形统计图和用样本估计总体,解题的关键是把条形统计图和扇形统计图的数据相结合求解.


科目:初中数学 来源: 题型:
【题目】某自行车公司调查阳光中学学生对其产品的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.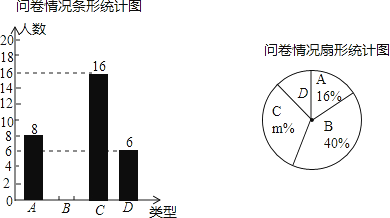
(1)本次问卷共随机调查了名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.
问题思考:
(1)如图1,一束光线从点A处入射到平面镜上,反射后恰好过点B,请在图中确定平面镜上的入射点P,保留作图痕迹,并简要说明理由;
(2)如图2,两平面镜OM、ON相交于点O,且OM⊥ON,一束光线从点A出发,经过平面镜反射后,恰好经过点B.小昕说,光线可以只经过平面镜OM反射后过点B,也可以只经过平面镜ON反射后过点B.除了小昕的两种做法外,你还有其它做法吗?如果有,请在图中画出光线的行进路线,保留作图痕迹,并简要说明理由;
问题拓展:
(3)如图3,两平面镜OM、ON相交于点O,且∠MON=30°,一束光线从点S出发,且平行于平面镜OM,第一次在点A处反射,经过若干次反射后又回到了点S,如果SA和AO的长均为1m,求这束光线经过的路程;
(4)如图4,两平面镜OM、ON相交于点O,且∠MON=15°,一束光线从点P出发,经过若干次反射后,最后反射出去时,光线平行于平面镜OM.设光线出发时与射线PM的夹角为θ(0°<θ<180°),请直接写出满足条件的所有θ的度数(注:OM、ON足够长)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=3,求△ABP的周长;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=_____.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求回答问题
(1)观察下列图形与等式的关系,并填空:
(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有n的代数式填空:
1+3+5+…+(2n﹣1)+()+(2n﹣1)+…+5+3+1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 ![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com