
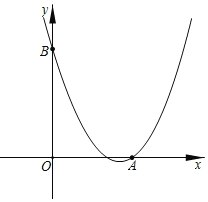
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与直线AB相交,与x轴、y轴交于A(2,0)、B(0,2![]() ).
).
(1)求点O关于AB的对称点P的坐标;
(2)若点P在二次函数y=ax2+bx+c(a≠0)的图象上,求二次函数y=ax2+bx+c(a≠0)的关系式.
(3)在(2)的条件下,在△ABP内存在点M,使得MA+MB+MP的值最小,则相应点M的坐标为 .
【答案】(1)点P(3,![]() );(2)y=﹣
);(2)y=﹣![]() x2+
x2+![]() x+2
x+2![]() ;(3)点M坐标为(
;(3)点M坐标为(![]() ,
,![]() ),
),
【解析】
(1)由tan∠BAO=![]() =
=![]() ,则∠BAO=60°,GA=
,则∠BAO=60°,GA=![]() OA=1,由∠GAP=∠PAH,得AH=AG=1,则PH=AHtan60°=
OA=1,由∠GAP=∠PAH,得AH=AG=1,则PH=AHtan60°=![]() ,即可求解;
,即可求解;
(2)将点A、B、P的坐标代入二次函数表达式,即可求解;
(3)△ABP为直角三角形,当点M与点G重合时,MA+MB+MP的值最小,即可求解.
(1)连接AB,过点O作OP⊥AB交AB于点G,过点P作PH⊥x轴于点H,
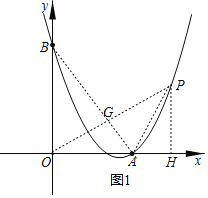
∵点O关于AB的对称点P,∴OG=PG,
tan∠BAO=![]() =
=![]() ,则∠BAO=60°,
,则∠BAO=60°,
则∠GOA=∠OAB=30°,∠GAO=∠GAP=∠PAH=60°,
则GA=![]() OA=1,∵∠GAP=∠PAH,∴AH=AG=1,
OA=1,∵∠GAP=∠PAH,∴AH=AG=1,
则PH=AHtan60°=![]() ,
,
故点P(3,![]() );
);
(2)将点A、B、P的坐标代入二次函数表达式得:
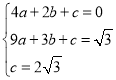 ,解得:
,解得: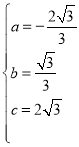 ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+2
x+2![]() ;
;
(3)连接PB,
由题意得:AB=4,AP=2,BP=![]() ,
,
则△ABP为直角三角形,
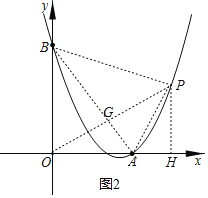
当点M与点G重合时,MA+MB+MP的值最小,
点M坐标为(![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
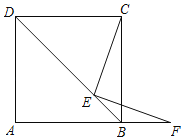
【题目】如图,在正方形ABCD中,E是对角线BD上一点,DE=4BE,连接CE,过点E作EF⊥CE交AB的延长线于点F,若AF=8,则正方形ABCD的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
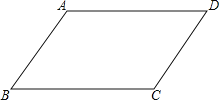
【题目】如图,在平行四边形ABCD中,
(1)以BD为对角线,作菱形MBND,使得M、N分别在BA、DC的延长线上.(保留作图痕迹,不写作图过程)
(2)证明所作四边形MBND是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
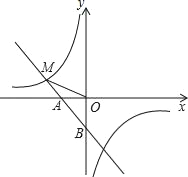
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com