
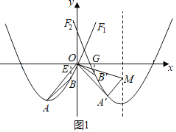
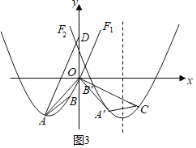
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
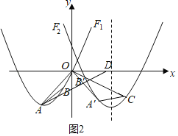
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.

【答案】(1)点A坐标为(﹣4,﹣4),点B坐标为(﹣1,﹣2);(2)S△OA'M=8;(3)点D坐标为(4,0)、(8,0)、(0,4)或(0,8)时,以A、O、D为顶点的三角形与△OA'C相似.
【解析】
(1)把x=﹣4代入解析式,求得点A的坐标,把y=-2代入解析式,根据点B与点A的位置关系即可求得点B的坐标;
(2)如图1,过点B作BE⊥x轴于点E,过点B'作B'G⊥x轴于点G,先求出点A'、B'的坐标,OA=OA'=![]() ,然后利用待定系数法求得抛物线F2解析式为:
,然后利用待定系数法求得抛物线F2解析式为:![]() ,对称轴为直线:
,对称轴为直线:![]() ,设M(6,m),表示出OM2,A'M2,进而根据OA'2+A'M2=OM2,得到(4
,设M(6,m),表示出OM2,A'M2,进而根据OA'2+A'M2=OM2,得到(4![]() )2+m2+8m+20=36+m2,求得m=﹣2,继而求得A'M=
)2+m2+8m+20=36+m2,求得m=﹣2,继而求得A'M=![]() ,再根据S△OA'M=
,再根据S△OA'M=![]() OA'A'M通过计算即可得;
OA'A'M通过计算即可得;
(3)在坐标轴上存在点D,使得以A、O、D为顶点的三角形与△OA'C相似,先求得直线OA与x轴夹角为45°,再分点D在x轴负半轴或y轴负半轴时,∠AOD=45°,此时△AOD不可能与△OA'C相似,点D在x轴正半轴或y轴正半轴时,∠AOD=∠OA'C=135°(如图2、图3),此时再分△AOD∽△OA'C,△DOA∽△OA'C两种情况分别讨论即可得.
(1)当x=﹣4时,![]() ,
,
∴点A坐标为(﹣4,﹣4),
当y=﹣2时,![]() ,
,
解得:x1=﹣1,x2=﹣6,
∵点A在点B的左侧,
∴点B坐标为(﹣1,﹣2);
(2)如图1,过点B作BE⊥x轴于点E,过点B'作B'G⊥x轴于点G,
∴∠BEO=∠OGB'=90°,OE=1,BE=2,
∵将△AOB绕点O逆时针旋转90°得到△A'OB',
∴OB=OB',∠BOB'=90°,
∴∠BOE+∠B'OG=∠BOE+∠OBE=90°,
∴∠B'OG=∠OBE,
在△B'OG与△OBE中
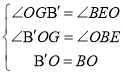 ,
,
∴△B'OG≌△OBE(AAS),
∴OG=BE=2,B'G=OE=1,
∵点B'在第四象限,
∴B'(2,﹣1),
同理可求得:A'(4,﹣4),
∴OA=OA'=![]() ,
,
∵抛物线F2:y=ax2+bx+4经过点A'、B',
∴![]() ,
,
解得: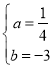 ,
,
∴抛物线F2解析式为:![]() ,
,
∴对称轴为直线: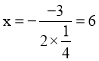 ,
,
∵点M在直线x=6上,设M(6,m),
∴OM2=62+m2,A'M2=(6﹣4)2+(m+4)2=m2+8m+20,
∵点A'在以OM为直径的圆上,
∴∠OA'M=90°,
∴OA'2+A'M2=OM2,
∴(4![]() )2+m2+8m+20=36+m2,
)2+m2+8m+20=36+m2,
解得:m=﹣2,
∴A'M=![]() ,
,
∴S△OA'M=![]() OA'A'M=
OA'A'M=![]() ;
;
(3)在坐标轴上存在点D,使得以A、O、D为顶点的三角形与△OA'C相似,
∵B'(2,﹣1),
∴直线OB'解析式为y=﹣![]() x,
x,
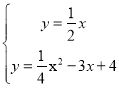 ,
,
解得: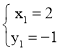 (即为点B'),
(即为点B'),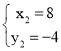 ,
,
∴C(8,﹣4),
∵A'(4,﹣4),
∴A'C∥x轴,A'C=4,
∴∠OA'C=135°,
∴∠A'OC<45°,∠A'CO<45°,
∵A(﹣4,﹣4),即直线OA与x轴夹角为45°,
∴当点D在x轴负半轴或y轴负半轴时,∠AOD=45°,此时△AOD不可能与△OA'C相似,
∴点D在x轴正半轴或y轴正半轴时,∠AOD=∠OA'C=135°(如图2、图3),
①若△AOD∽△OA'C,
则![]() ,
,
∴OD=A'C=4,
∴D(4,0)或(0,4);
②若△DOA∽△OA'C,
则![]() ,
,
∴OD=![]() OA'=8,
OA'=8,
∴D(8,0)或(0,8),
综上所述,点D坐标为(4,0)、(8,0)、(0,4)或(0,8)时,以A、O、D为顶点的三角形与△OA'C相似.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“共点抛物线”,这个交点为“共点”.
(1)判断抛物线y=x2与y=﹣x2是“共点抛物线”吗?如果是,直接写出“共点”坐标;如果不是,说明理由;
(2)抛物线y=x2﹣2x与y=x2﹣2mx﹣3是“共点抛物线”,且“共点”在x轴上,求抛物线y=x2﹣2mx﹣3的函数关系式;
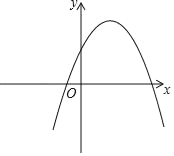
(3)抛物线L1:y=﹣x2+2x+1的图象如图所示,L1与L2:y=﹣2x2+mx是“共点抛物线”;
①求m的值;
②点P是x轴负半轴上一点,设抛物线L1、L2的“共点”为Q,作点P关于点Q的对称点P′,以PP′为对角线作正方形PMP′N,当点M或点N落在抛物线L1上时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某学校为构建书香校园,拟购进甲、乙两种规格的书柜放置新购置的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台.
(1)求甲、乙两种书柜的进价;
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.请您帮该校设计一种购买方案,使得花费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博园开放后,前往参观的人非常多.5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是__________;
(2)求表中a、b、c的值,并请补全频数分布直方图;
(3)在调查人数里,等候时间少于40min的有人___________;
(4)此次调查中,中位数所在的时间段是__________~__________min.
时间分段/min | 频数/人数 | 频率 |
10~20 | 8 | 0.200 |
20~30 | 14 | a |
30~40 | 10 | 0.250 |
40~50 | b | 0.125 |
50~60 | 3 | 0.075 |
合计 | c | 1.000 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与直线AB相交,与x轴、y轴交于A(2,0)、B(0,2![]() ).
).
(1)求点O关于AB的对称点P的坐标;
(2)若点P在二次函数y=ax2+bx+c(a≠0)的图象上,求二次函数y=ax2+bx+c(a≠0)的关系式.
(3)在(2)的条件下,在△ABP内存在点M,使得MA+MB+MP的值最小,则相应点M的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于点P.
(1)求证:AC2=ADAB.
(2)点E是∠ACB所对的弧上的一个动点(不包括A,B两点),连接EC交直径AB于点F,∠DAP=64°.
①当∠ECB= °时,△PCF为等腰三角形;
②当∠ECB= °时,四边形ACBE为矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com