
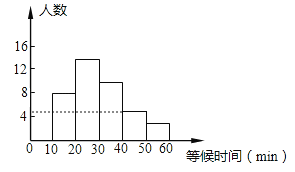
ЁОЬтФПЁПЩЯКЃЪРВЉдАПЊЗХКѓЃЌЧАЭљВЮЙлЕФШЫЗЧГЃЖр.5дТжабЎЕФвЛЬьФГвЛЪБЖЮЃЌЫцЛњЕїВщСЫВПЗжШыдАгЮПЭЃЌЭГМЦСЫЫћУЧНјдАЧАЕШКђМьЦБЕФЪБМфЃЌВЂЛцжЦГЩШчЯТЭМБэ.БэжаЁА10~20ЁББэЪОЕШКђМьЦБЕФЪБМфДѓгкЛђЕШгк10minЖјаЁгк20minЃЌЦфЫќРрЭЌ.
ЃЈ1ЃЉетРяВЩгУЕФЕїВщЗНЪНЪЧ__________ЃЛ
ЃЈ2ЃЉЧѓБэжаaЁЂbЁЂcЕФжЕЃЌВЂЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉдкЕїВщШЫЪ§РяЃЌЕШКђЪБМфЩйгк40minЕФгаШЫ___________ЃЛ
ЃЈ4ЃЉДЫДЮЕїВщжаЃЌжаЮЛЪ§ЫљдкЕФЪБМфЖЮЪЧ__________~__________min.
ЪБМфЗжЖЮ/min | ЦЕЪ§/ШЫЪ§ | ЦЕТЪ |
10~20 | 8 | 0.200 |
20~30 | 14 | a |
30~40 | 10 | 0.250 |
40~50 | b | 0.125 |
50~60 | 3 | 0.075 |
КЯМЦ | c | 1.000 |

ЁОД№АИЁПГщбљЕїВщЛђГщВщЃЈЬюЁАГщбљЁБвВПЩвдЃЉ a=0.350ЃЛb=5ЃЛc=40ЃЛЦЕЪ§ЗжВМжБЗНЭММћНтЮі 32 20ЃЌ30
ЁОНтЮіЁП
ЃЈ1ЃЉгЩгкЧАЭљВЮЙлЕФШЫЗЧГЃЖрЃЌ5дТжабЎЕФвЛЬьФГвЛЪБЖЮЃЌЫцЛњЕїВщСЫВПЗжШыдАгЮПЭЃЌЭГМЦСЫЫћУЧНјдАЧАЕШКђМьЦБЕФЪБМфЃЌгЩДЫМДПЩХаЖЯЕїВщЗНЪНЃЛ
ЃЈ2ЃЉЪзЯШИљОнвбжЊЕФвЛзщЪ§ОнПЩвдЧѓГіНгЪмЕїВщЕФзмШЫЪ§cЃЌШЛКѓГЫвдЦЕТЪМДПЩЧѓГіbЃЌРћгУЫљгаЦЕТЪжЎКЭЮЊ1МДПЩЧѓГіaЃЌШЛКѓОЭПЩвдВЙШЋЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉИљОнБэИёжЊЕРБЛЕїВщШЫЪ§РяЃЌЕШКђЪБМфЩйгк40minЕФгаЕквЛЁЂЖўЁЂШ§аЁзщЃЌРћгУБэИёЪ§ОнМДПЩЧѓГіЕШКђЪБМфЩйгк40minЕФШЫЪ§ЃЛ
ЃЈ4ЃЉгЩгкжЊЕРзмШЫЪ§ЮЊ40ШЫЃЌИљОнжаЮЛЪ§ЕФЖЈвхОЭПЩвджЊЕРжаЮЛЪ§ТфдкФФИіаЁзщЃЎ
ЃЈ1ЃЉЬюГщбљЕїВщЛђГщВщЃЛ
ЃЈ2ЃЉЁпa=1Љ0.200Љ0.250Љ0.125Љ0.075=0.350ЃЛ
b=8ЁТ0.200ЁС0.125=5ЃЛ
c=8ЁТ0.200=40ЃЛ
ЦЕЪ§ЗжВМжБЗНЭМШчЭМЫљЪОЃЎ
ЃЈ3ЃЉвРЬтвтЕУЃК
дкЕїВщШЫЪ§РяЃЌЕШКђЪБМфЩйгк40minЕФга8+14+10=32ШЫЃЎ
ЙЪД№АИЮЊЃК32ЃЎ
ЃЈ4ЃЉЁпзмШЫЪ§ЮЊ40ШЫЃЌЁржаЮЛЪ§ЫљдкЕФЪБМфЖЮЪЧ20ЁЋ30ЃЎ
ЙЪД№АИЮЊЃК20ЃЌ30ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНижС2019Фъ5дТЃЌЩНЮїЪЁеўИЎДѓСІЪЕЪЉЕФНЈЩшЁАЩНЮїХЉЙШЁБеНТдГЩЙћГѕЯжЃЌЁАЩНЮїХЉЙШЁБЭЈЙ§зщНЈЩНЮїХЉЙШЩњЮяПЦММбаОПдКЃЌж№ВННЈГЩДѓбЇЩњЁАЛЅСЊЭј+ХЉвЕЁБДДаТДДвЕдАЃЎФГаЃПЦММаЁзщЕНИУДДвЕдАЕФШЋЛЗОГжЧФмЗЌЧбЬиЩЋаЁеђНјаазлКЯЪЕМљЛюЖЏЃЌЫцЛњЕїВщСЫ60жъЁАХЉЙШвЛКХЁАЗЌЧбЕФЙвЙћЪ§СПЃЈЕЅЮЛЃКИіЃЉЃЌВЂЛцжЦСЫШчЯТВЛЭъППЕФЭГМЦЭМБэЃК
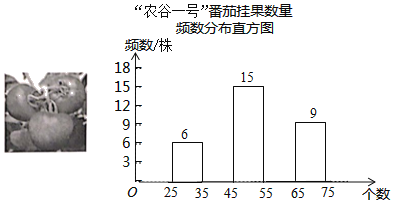
ЁАХЉЙШвЛКХЁБЗЌЧбЙвЙћЪ§СПЭГМЦБэ
ЙвЙћЪ§СПxЃЈИіЃЉ | ЦЕЪ§ЃЈжъЃЉ | ЦЕТЪ |
25ЁмЃМ35 | 6 | |
35ЁмxЃМ45 | 0.2 | |
45ЁмxЃМ55 | 15 | a |
55ЁмxЃМ65 | ||
65ЁмxЃМ75 | 9 |
ЧыНсКЯЭМБэжаЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈlЃЉЭГМЦБэжаЃЌaЃНЁЁ ЁЁЃЌШєЛцжЦЁАХЉЙШвЛКХЁБЗЌЧбЙвЙћЪ§СПЩШаЮЭГМЦЭМЃЌдђЙвЙћЪ§СПдкЁА35ЁмxЃМ45ЁБЫљЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєЫљжжжВЕФЁАХЉЙШвЛКХЁБЗЌЧбга1000жъЃЌЧыЙРМЦЙвЙћЪ§СПдкЁА55ЁмxЃМ65ЁБЗЖЮЇЕФЗЌЧбжъЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФБпГЄЮЊ2ЃЌЕу
ЕФБпГЄЮЊ2ЃЌЕу![]() дк
дк![]() ЩЯЃЌЫФБпаЮ
ЩЯЃЌЫФБпаЮ![]() вВЪЧе§ЗНаЮЃЌвд
вВЪЧе§ЗНаЮЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЛ
ГЄЮЊАыОЖЛ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌ
ЃЌ![]() ЃЌдђЭМжавѕгАВПЗжУцЛ§ЮЊЃЈ ЃЉ
ЃЌдђЭМжавѕгАВПЗжУцЛ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌвбжЊADЃН10cmЃЌtanBЃН2ЃЌAEЁЭBCгкЕуEЃЌЧвAEЃН4cmЃЌЕуPЪЧBCБпЩЯвЛЖЏЕуЃЎШєЁїPADЮЊжБНЧШ§НЧаЮЃЌдђBPЕФГЄЮЊ_____

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїAOBЕФШ§ИіЖЅЕуAЁЂOЁЂBЗжБ№ТфдкХзЮяЯпF1ЃК![]() ЕФЭМЯѓЩЯЃЌЕуAЕФКсзјБъЮЊЉ4ЃЌЕуBЕФзнзјБъЮЊЉ2.(ЕуAдкЕуBЕФзѓВр)
ЕФЭМЯѓЩЯЃЌЕуAЕФКсзјБъЮЊЉ4ЃЌЕуBЕФзнзјБъЮЊЉ2.(ЕуAдкЕуBЕФзѓВр)
(1)ЧѓЕуAЁЂBЕФзјБъЃЛ
(2)НЋЁїAOBШЦЕуOФцЪБеыа§зЊ90ЁуЕУЕНЁїA'OB'ЃЌХзЮяЯпF2ЃК![]() ОЙ§A'ЁЂB'СНЕуЃЌвбжЊЕуMЮЊХзЮяЯпF2ЕФЖдГЦжсЩЯвЛЖЈЕуЃЌЧвЕуA'ЧЁКУдквдOMЮЊжБОЖЕФдВЩЯЃЌСЌНгOMЁЂA'MЃЌЧѓЁїOA'MЕФУцЛ§ЃЛ
ОЙ§A'ЁЂB'СНЕуЃЌвбжЊЕуMЮЊХзЮяЯпF2ЕФЖдГЦжсЩЯвЛЖЈЕуЃЌЧвЕуA'ЧЁКУдквдOMЮЊжБОЖЕФдВЩЯЃЌСЌНгOMЁЂA'MЃЌЧѓЁїOA'MЕФУцЛ§ЃЛ
(3)ШчЭМ2ЃЌбгГЄOB'НЛХзЮяЯпF2гкЕуCЃЌСЌНгA'CЃЌдкзјБъжсЩЯЪЧЗёДцдкЕуDЃЌЪЙЕУвдAЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїOA'CЯрЫЦ.ШєДцдкЃЌЧыЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЮЊСЫРЉДѓОгЊЃЌОіЖЈЙКНј6ЬЈЛњЦїгУгкЩњВњФГЛюШћЃЎЯжгаМзЁЂввСНжжЛњЦїЙЉбЁдёЃЌЦфжаУПжжЛњЦїЕФМлИёКЭУПЬЈЛњЦїШеЩњВњЛюШћЕФЪ§СПШчЯТБэЫљЪОЃЎОЙ§дЄЫуЃЌБОДЮЙКТђЛњЦїЫљКФзЪН№ВЛФмГЌЙ§34ЭђдЊ.
Мз | вв | |
МлИё(ЭђдЊ/ЬЈ) | 7 | 5 |
УПЬЈШеВњСП(Иі) | 100 | 60 |
(1)АДИУЙЋЫОвЊЧѓПЩвдгаМИжжЙКТђЗНАИЃП
(2)ШчЙћИУЙЋЫОЙКНјЕФ6ЬЈЛњЦїЕФШеЩњВњФмСІВЛФмЕЭгк380ИіЃЌФЧУДЮЊСЫНкдМзЪН№гІбЁдёЪВУДбљЕФЙКТђЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊКыбяжаЛЊгХауДЋЭГЮФЛЏЃЌФГаЃПЊеЙЁАОЕфЫаЖСЁББШШќЛюЖЏЃЌЫаЖСВФСЯгаЁЖТлгяЁЗЁЂЁЖДѓбЇЁЗЁЂЁЖжагЙЁЗЃЈвРДЮгУзжФИAЃЌBЃЌCБэЪОетШ§ИіВФСЯЃЉЃЌНЋAЃЌBЃЌCЗжБ№аДдк3еХЭъШЋЯрЭЌЕФВЛЭИУїПЈЦЌЕФе§УцЩЯЃЌБГУцГЏЩЯЯДдШКѓЗХдкзРУцЩЯЃЌБШШќЪБаЁРёЯШДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧЯТФкШнКѓЗХЛиЃЌЯДдШКѓЃЌдйгЩаЁжЧДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌЫћСЉАДИїздГщШЁЕФФкШнНјааЫаЖСБШШќЃЎ
ЃЈ1ЃЉаЁРёЫаЖСЁЖТлгяЁЗЕФИХТЪЪЧЁЁ ЁЁЃЛЃЈжБНгаДГіД№АИЃЉ
ЃЈ2ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЫћСЉЫаЖССНИіВЛЭЌВФСЯЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпГЄЮЊ4cmЃЌЁЯAЃН60ЁуЃЌЛЁBDЪЧвдЕуAЮЊдВаФЃЌABГЄЮЊАыОЖЕФЛЁЃЌЛЁCDЪЧвдЕуBЮЊдВаФЃЌBCГЄЮЊАыОЖЕФЛЁЃЌдђвѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
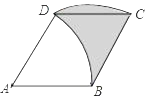
A. 2cm2B. 4![]() cm2C. 4cm2D. Іаcm2
cm2C. 4cm2D. Іаcm2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
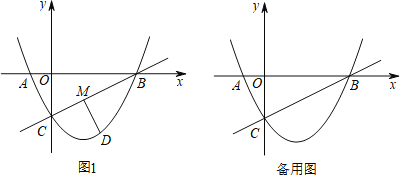
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃН![]() xЉ2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЖўДЮКЏЪ§yЃН
xЉ2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЖўДЮКЏЪ§yЃН![]() x2+bx+cЕФЭМЯѓОЙ§BЃЌCСНЕуЃЌЧвгыxжсЕФИКАыжсНЛгкЕуAЃЎ
x2+bx+cЕФЭМЯѓОЙ§BЃЌCСНЕуЃЌЧвгыxжсЕФИКАыжсНЛгкЕуAЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуMЪЧЯпЖЮBCЩЯЕФвЛЖЏЕуЃЌЖЏЕуDдкжБЯпBCЯТЗНЕФЖўДЮКЏЪ§ЭМЯѓЩЯЃЎЩшЕуDЕФКсзјБъЮЊmЃЎ
ЂйЙ§ЕуDзїDMЁЭBCгкЕуMЃЌЧѓЯпЖЮDMЙигкmЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓЯпЖЮDMЕФзюДѓжЕЃЛ
ЂкШєЁїCDMЮЊЕШбќжБНЧШ§НЧаЮЃЌжБНгаДГіЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com