
【题目】在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点B,与y轴交于点C,二次函数y=
x﹣2与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的解析式;
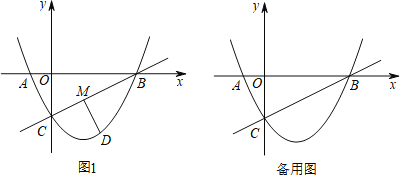
(2)如图1,点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.
①过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;
②若△CDM为等腰直角三角形,直接写出点M的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)①DM=﹣
x﹣2;(2)①DM=﹣![]() ,DM的最大值为
,DM的最大值为![]() ;②M的坐标为(
;②M的坐标为(![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)由直线y=![]() x﹣2得B(4,0)、C(0,﹣2),将B(4,0)、C(0,﹣2)代入y=
x﹣2得B(4,0)、C(0,﹣2),将B(4,0)、C(0,﹣2)代入y=![]() x2+bx+c,列方程组求出b、c即可;
x2+bx+c,列方程组求出b、c即可;
(2)①过点DH∥AB,交直线y=![]() x﹣2于点H.则∠H=∠OBC,OC=2,OB=4,BC=2
x﹣2于点H.则∠H=∠OBC,OC=2,OB=4,BC=2![]() ,由sin∠H=sin∠OBC=
,由sin∠H=sin∠OBC=![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,设D(m,
,设D(m,![]() m2﹣
m2﹣![]() m﹣2),则H(m2﹣3m,
m﹣2),则H(m2﹣3m,![]() m2﹣
m2﹣![]() m﹣2),DH=m﹣(m2﹣3m)=﹣m2+4m,所以DM=
m﹣2),DH=m﹣(m2﹣3m)=﹣m2+4m,所以DM=![]() (﹣m2+4m)=﹣
(﹣m2+4m)=﹣![]() ,当m=2时,DM的最大值为
,当m=2时,DM的最大值为![]() ;
;
②分两种情况:当CM⊥DM时,过点M作ME⊥y轴于点E,点D作DF∥y轴,交EM的延长线于点F;当CD⊥DM时,过点D作DE⊥y轴于点E,点M作MF∥y轴,交ED的延长线于点F,分别求出t的值即可.
解(1)由直线y=![]() x﹣2得
x﹣2得
B(4,0)、C(0,﹣2),
将B(4,0)、C(0,﹣2)代入y=![]() x2+bx+c,
x2+bx+c,
![]() ,
,
解得b=![]() ,c=﹣2,
,c=﹣2,
∴二次函数的解析式y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)①过点DH∥AB,交直线y=![]() x﹣2于点H.
x﹣2于点H.

∴∠H=∠OBC,
∵B(4,0)、C(0,﹣2),
∴OC=2,OB=4,BC=2![]()
∴sin∠H=sin∠OBC=![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() ,
,
设D(m,![]() m2﹣
m2﹣![]() m﹣2),则H(m2﹣3m,
m﹣2),则H(m2﹣3m,![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∴DH=m﹣(m2﹣3m)=﹣m2+4m,
∴DM=![]() (﹣m2+4m)=﹣
(﹣m2+4m)=﹣![]() ,
,
当m=2时,DM的最大值为![]() ;
;
②Ⅰ.当CM⊥DM时,过点M作ME⊥y轴于点E,点D作DF∥y轴,交EM的延长线于点F,
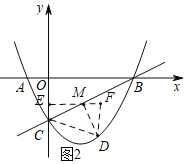
∵△CDM为等腰直角三角形,易证△EMC≌△FDM,
∴EM=DF,EC=MF,
设M(t,![]() t﹣2),则EM=t,OE=﹣
t﹣2),则EM=t,OE=﹣![]() t+2,
t+2,
∴CE=OC﹣OE=2﹣(﹣![]() t+2)=
t+2)=![]() t,MF=
t,MF=![]() t,DF=t,
t,DF=t,
EF=EM+MF=t+![]() t=
t=![]() ,OE+DF=﹣
,OE+DF=﹣![]() t+2+t=
t+2+t=![]() t+2,
t+2,
∴D(![]() t,﹣
t,﹣![]() t﹣2)
t﹣2)
将D(![]() t,﹣
t,﹣![]() t﹣2)代入二次函数的解析式y=
t﹣2)代入二次函数的解析式y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
![]() ,
,
解得t=0(舍去)或t=![]() ,
,
∴M1(![]() );
);
Ⅱ.当CD⊥DM时,过点D作DE⊥y轴于点E,点M作MF∥y轴,交ED的延长线于点F,
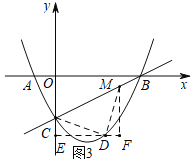
∵△CDM为等腰直角三角形,易证△CED≌△DFM,
∴DE=MF,EC=DF,
设M(t,![]() t﹣2),则EF=t,CE=
t﹣2),则EF=t,CE=![]() ,DE=
,DE=![]() t,MF=
t,MF=![]() t,OC=
t,OC=![]() t+2
t+2
∴D(![]() t,﹣
t,﹣![]() t﹣2),
t﹣2),
将D(![]() t,﹣
t,﹣![]() t﹣2)代入二次函数的解析式y=
t﹣2)代入二次函数的解析式y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
![]() ,
,
解得t=0(舍去)或t=![]() ,
,
∴M2(![]() ,﹣
,﹣![]() )
)
综上,△CDM为等腰直角三角形,点M的坐标为(![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】上海世博园开放后,前往参观的人非常多.5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是__________;
(2)求表中a、b、c的值,并请补全频数分布直方图;
(3)在调查人数里,等候时间少于40min的有人___________;
(4)此次调查中,中位数所在的时间段是__________~__________min.
时间分段/min | 频数/人数 | 频率 |
10~20 | 8 | 0.200 |
20~30 | 14 | a |
30~40 | 10 | 0.250 |
40~50 | b | 0.125 |
50~60 | 3 | 0.075 |
合计 | c | 1.000 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=BC=10,点D,E在线段BC上,且CD=2,BE=5,点P,Q分别是线段AC,AB上的动点,则四边形PQED周长的最小值为_____.
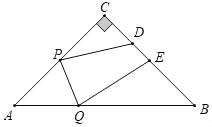
查看答案和解析>>
科目:初中数学 来源: 题型:
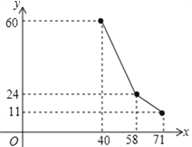
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于点P.
(1)求证:AC2=ADAB.
(2)点E是∠ACB所对的弧上的一个动点(不包括A,B两点),连接EC交直径AB于点F,∠DAP=64°.
①当∠ECB= °时,△PCF为等腰三角形;
②当∠ECB= °时,四边形ACBE为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形;

求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.

老师说:“小凯的作法正确”.
回答下列问题:
根据小凯的做法,小明将题目改编为一道证明题,请你帮助小明完成下列步骤:
(1)已知:在平行四边形ABCD中,点E、F分别在边BC、AD上, .(补全已知条件)
求证:四边形AECF是菱形.
(2)证明:(写出证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:

(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com