
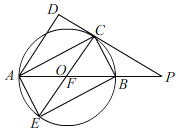
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于点P.
(1)求证:AC2=ADAB.
(2)点E是∠ACB所对的弧上的一个动点(不包括A,B两点),连接EC交直径AB于点F,∠DAP=64°.
①当∠ECB= °时,△PCF为等腰三角形;
②当∠ECB= °时,四边形ACBE为矩形.

【答案】(1)见解析;(2)①45;②58.
【解析】
(1)先判断出∠ACD=∠ABC,再利用直径所对的圆周角等于90度和垂直的定义判断出∠ADC=∠ACB,进而判断出△ADC∽△ACB,即可得出结论;
(2)①先求出∠CAD=32°,判断出∠CAP>∠P,进而判断出CF≠CP,再求出∠BCP=32°>∠P,得出BP>BC,进而判断出CF≠PF,最后用等腰三角形的性质即可得出结论;
②先判断出CE过点O,进而求出∠ACE,即可得出结论.
解:(1)∵CD是⊙O的切线,
∴∠ACD=∠ABC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD⊥CD,
∴∠ADC=90°=∠ACB,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ABAD;
(2)①由(1)知,∠ACD=∠ABC,
∵∠ACD+∠CAD=90°,∠ABC+∠BAC=90°,
∴∠CAD=∠BAC=![]() ∠DAP=32°,
∠DAP=32°,
∵∠P=90°﹣∠DAP=26°,
∴∠CAP>∠P,
∴CP>AC,
∵点F在直径AB上(且不和点A,B重合),
∴CF≠CP,
∵∠CAD=32°,
∴∠ACD=90°﹣∠CAD=58°,
∵∠ACB=90°,
∴∠BCP=180°﹣∠ACD﹣∠ACB=32°>∠P
∴BP>BC,
∵点F在直径AB上(且不和点A,B重合),
∴CF≠PF,
∵△PCF是等腰三角形,
∴PC=PF,
∴∠PCF=![]() (180°﹣∠P)=77°,
(180°﹣∠P)=77°,
∴∠BCE=∠PCF﹣∠BCP=45°,
故答案为:45;
②如图,
∵四边形ACBE是矩形,
∴AB与CE互相平分,
∵点O是AB的中点,
∴点F和点O重合,
∴∠ACE=∠CAB=32°,
∴∠BCE=90°﹣∠ACE=58°,
故答案为:58.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
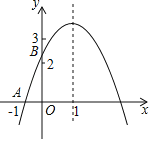
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
①当﹣1<x<3时,y>0;②﹣1<a<﹣![]() ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0) .以D为顶点的抛物线y = ax2+bx+c过点B. 动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒. 过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.

(1)求抛物线的解析式;
(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?
(3)动点P、Q运动过程中,在矩形ABCD内(包括其边界)是否存在点H,使以B,Q,E,H为顶点的四边形是菱形,若存在,请直接写出此时菱形的周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
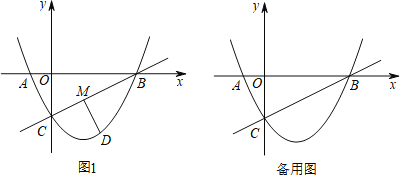
【题目】在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点B,与y轴交于点C,二次函数y=
x﹣2与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的解析式;
(2)如图1,点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.
①过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;
②若△CDM为等腰直角三角形,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com