
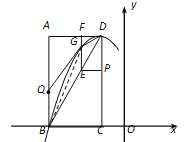
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������A(��3��4)��B(��3��0)��C(��1��0) .��DΪ�����������y = ax2+bx+c����B. ����P�ӵ�D��������DC�����C�˶���ͬʱ����Q�ӵ�B��������BA�����A�˶�����P��Q�˶����ٶȾ�Ϊÿ��1����λ���˶���ʱ��Ϊt��. ����P��PE��CD��BD�ڵ�E������E��EF��AD�ڵ�F�����������ڵ�G.

��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ���ı���BDGQ�����������ֵΪ���٣�
��3������P��Q�˶������У��ھ���ABCD�ڣ�������߽磩�Ƿ���ڵ�H��ʹ��B��Q��E��HΪ������ı��������Σ������ڣ���ֱ��д����ʱ���ε��ܳ����������ڣ���˵������.
���𰸡���1��y=��x2��2x��3��2����t =2ʱ���ı���BDGQ�����������ֵΪ2��3�����ڣ� ![]() ��80��32
��80��32![]()
�������������������1�����ݾ��ε����ʿ���д����D�õ����ꣻ�ɶ���D���������������ߵĶ���ʽ����Ϊy=a��x+1��2+4��Ȼ��B��������룬�������ϵ��a��ֵ�����ô���ϵ�����������ߵĽ���ʽ������2������������������DPE�ס�DBC������õ�E�ĺ����꣬�����AF�ij���������������������G�ĺ����ꣻȻ���������߷��̡�ͼ��������任�������GE=![]() �����������ε������ʽ������ã�S�ı���BDGQ= S��BQG��S��BEG��S��DEG���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ2;��3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϡ���CE�DZߺͶԽ�������������ۼ��ɡ�
�����������ε������ʽ������ã�S�ı���BDGQ= S��BQG��S��BEG��S��DEG���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ2;��3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϡ���CE�DZߺͶԽ�������������ۼ��ɡ�
���������
��1�� ������ã�����D�������Ϊ����1��4��.
�������ߵĽ���ʽΪy=a (x��1) 2��4��a��0����
�������߾�����B(��3��0)������y=a (x��1) 2��4
�����a=��1
�������ߵĽ���ʽΪy=�� (x��1) 2��4
��y=��x2��2x��3.
��2��������֪��DP=BQ = t��
��PE��BC��
���DPE�ס�DBC.
��![]() =2��
=2��
��PE=![]() DP=
DP= ![]() t.
t.
���E�ĺ�����Ϊ��1��![]() t��AF=2��
t��AF=2��![]() t.
t.
��x =��1��![]() t����y=�� (x��1) 2��4����y=��
t����y=�� (x��1) 2��4����y=��![]() t2��4.
t2��4.
���G����������![]() t2��4��
t2��4��
��GE=![]() t2��4����4��t��=��
t2��4����4��t��=��![]() t2��t.
t2��t.
����BG��S�ı���BDGQ= S��BQG��S��BEG��S��DEG��
��S�ı���BDGQ=![]() BQ��AF��
BQ��AF��![]() EG����AF��DF��
EG����AF��DF��
=![]() t��2��
t��2��![]() t����
t����![]() t2��t.
t2��t.
=��![]() t2��2t=��
t2��2t=��![]() (t��2)2��2.
(t��2)2��2.
�൱t =2ʱ���ı���BDGQ�����������ֵΪ2.
��3�����ڣ�
����BQEH���ܳ�Ϊ![]() ��80��32
��80��32![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACE����ABCD�ĶԽ���ACΪ�ߵĵȱ������Σ���C���E����x��Գƣ���E��������ǣ�7����3 ![]() ������D��������� ��
������D��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��A����ˮ��ˮ·��ΪAB���ֽ��и��죬��·��AO����ܵ����������ܵ�BO���ӣ�AO��BO��������·��AO��̣����������ͣ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ��������ABCֽƬ����D��E�ֱ��ǡ�ABC�������㣮 �о���1���������ֱ��DE�۵���ʹA������CE�ϣ����BDA�����A��������ϵ��
�о���2��������۳�ͼ2����״�������BDA�䡢��CEA��͡�A��������ϵ��
�о���3��������۳�ͼ3����״�������BDA�䡢��CEA��͡�A��������ϵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ک�3.5�� ![]() ��0��
��0�� ![]() ����
���� ![]() ��
�� ![]() ��0.161161116������������ ������
��0.161161116������������ ������
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˶���ʽ������ת���ǣ� ��
A.�ӱ����Ӱڵİڶ�
B.Ͷ������������˶�
C.����ʮ��������յ��˶�
D.������������λ�õı仯
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ� 
��1�����̶�����ľ��AB��BC��AD������AB=AD=2cm��BC=5cm����ͼ�����õ��ĸ�ľ��CD=5cm���жϴ�ʱ��B���D�Ƿ���ȣ���˵�����ɣ�
��2�����̶�һ��ľ��AB������AB=2cm������ľ��CD=5cm�����ľ��AD��BC�ij��Ȳ��䣬����D�Ƶ�BA���ӳ�����ʱ����CҲ��BA���ӳ����ϣ�����C�Ƶ�AB���ӳ�����ʱ����A��C��D�ܹ����ܳ�Ϊ30cm�������Σ����ľ��AD��BC�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com