
【题目】我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“共点抛物线”,这个交点为“共点”.
(1)判断抛物线y=x2与y=﹣x2是“共点抛物线”吗?如果是,直接写出“共点”坐标;如果不是,说明理由;
(2)抛物线y=x2﹣2x与y=x2﹣2mx﹣3是“共点抛物线”,且“共点”在x轴上,求抛物线y=x2﹣2mx﹣3的函数关系式;
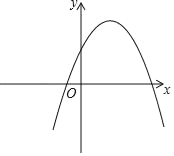
(3)抛物线L1:y=﹣x2+2x+1的图象如图所示,L1与L2:y=﹣2x2+mx是“共点抛物线”;
①求m的值;
②点P是x轴负半轴上一点,设抛物线L1、L2的“共点”为Q,作点P关于点Q的对称点P′,以PP′为对角线作正方形PMP′N,当点M或点N落在抛物线L1上时,直接写出点P的坐标.
【答案】(1)是,(0,0);(2)![]() ;(3)①m的值为0或4,②P(﹣3,0)或P(﹣5,0)或P(﹣13,0).
;(3)①m的值为0或4,②P(﹣3,0)或P(﹣5,0)或P(﹣13,0).
【解析】
(1)解方程x2=﹣x2得出x=0
(2)因为两个抛物线的共点在x轴上,y=0代入L1中求得交点坐标,分别代入L2中,求得m的值,获得抛物线的解析式.
(3)①两抛物线为共点抛物线时,只有一个交点,运用判别式为零,求出m的值
②设点P坐标(a,0),通过Q点坐标,获得P'点坐标,因为PP'为正方形,利用K型全等模型建立全等关系,从而求出点M和N的坐标,将M、N分别代入解析式,获得a的值,从而求出点P的坐标.
解:(1)是,(0,0)
x2=﹣x2
∴x=0
(2)令y=x2﹣2x=0
解得x1=0,x2=2
当x=0时,﹣3≠0
∴(0,0)不是共点
当x=2时,4﹣4m﹣3=0
解得m=![]()
∴y=![]()
(3)①若两个抛物线是“共点抛物线”
则方程﹣x2+2x+1=﹣2x2+mx有两个相等的实数根
即x2+(2﹣m)x+1=0有两个相等的实数根
∴△=(2﹣m)2﹣4=0
解得m=0或m=4
∴m的值为0或4.
②P(﹣3,0)或P(﹣5,0)或P(﹣13,0)
设点P(a,0)
当m=0时,Q(﹣1,﹣2)
∴P'(﹣2﹣a,﹣4)
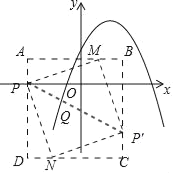
∵PM=MP',∠A=∠B,∠AMP=∠BP'M
∴△APM≌△BMP'(AAS)
设M(x,y),N(a,b)
![]() 解得
解得![]()
![]() 解得
解得![]()
∴可得M(1,﹣3﹣a),N(﹣3,a﹣1)
分别代入L1解析式可得
a1=﹣5,a2=﹣13
当m=4时,Q(1,2)
∴P'(2﹣a,4)
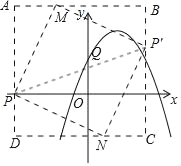
∵PM=MP',∠A=∠B,∠AMP=∠BP'M
∴△APM≌△BMP'(AAS)
设M(m,n)N(x,y)
![]() 解得
解得![]()
![]() 解得
解得![]()
∴可得M(﹣2,4﹣a),N(3,1+a)
分别代入L1解析式可得
a1=﹣3,a2=11(舍)
∴P(﹣3,0)或P(﹣5,0)或P(﹣13,0)


科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 与反比例函数的图象交于点
与反比例函数的图象交于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
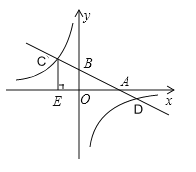
(1)求反比例函数及一次函数的解析式.
(2)当![]() 为何值时一次函数的值大于反比例函数的值.
为何值时一次函数的值大于反比例函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第五代移动电话通信行动标准,也称第五代移动通信技术,外语缩写:5G.也是4G之后的延伸,正在研究中,5G网络的理论下行速度为10Gb/s(相当于下载速度1.25GB/s).2019年1月24日,华为发布了迄今最强大的5G基带芯片Balong500,同时,还发布了全球最快CPE,支持智能家居连接.中国5G技术的研发带来了社会生产力和社会关系的重大改变,它是国人的骄傲….小明组织了几位同学就5G手机面世后自己居住的小区使用手机的居民是否立即改用5G手机问题,随机对本小区的部分使用手机的居民进行了问卷调查(分五类:A表示非常期待体验,将立即使用;B表示担心费用太高消费不起,但还是要体验,将立即使用;C表示怕技术不成熟,造成经济损失,但还是要体验,将立即使用;D表示先等待一段时间后再说,暂时不体验,不立即使用;E表示其它原因不体验,不立即使用).根据调查结果分别绘制了如下两个统计图,请根据图中提供的信息解答下列问题:

(1)随机被调查的居民总人数为 人,m= ,扇形统计图中A类所对应扇形的园心角为 度;
(2)请根据统计数据补全条形统计图;
(3)若小区有使用手机的居民共约8000人,请估计约有多少居民在5G手机面世后不立即使用5G手机?若通讯公司在5G手机面世后第一个月在本小区的业务目标是最多2000手机用户不使用5G手机,请根据计算结果帮助公司拟定一条宣传建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至2019年5月,山西省政府大力实施的建设“山西农谷”战略成果初现,“山西农谷”通过组建山西农谷生物科技研究院,逐步建成大学生“互联网+农业”创新创业园.某校科技小组到该创业园的全环境智能番茄特色小镇进行综合实践活动,随机调查了60株“农谷一号“番茄的挂果数量(单位:个),并绘制了如下不完靠的统计图表:
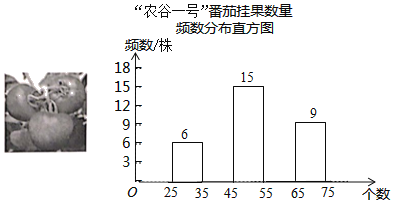
“农谷一号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤<35 | 6 | |
35≤x<45 | 0.2 | |
45≤x<55 | 15 | a |
55≤x<65 | ||
65≤x<75 | 9 |
请结合图表中的信息解答下列问题:
(l)统计表中,a= ,若绘制“农谷一号”番茄挂果数量扇形统计图,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 ;
(2)将频数分布直方图补充完整;
(3)若所种植的“农谷一号”番茄有1000株,请估计挂果数量在“55≤x<65”范围的番茄株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com