
����Ŀ����ͼ��1������![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��������һ�㣬
��������һ�㣬![]() Ϊ
Ϊ![]() ��һ���㣬�ֱ���
��һ���㣬�ֱ���![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() �͵ȱ�������
�͵ȱ�������![]() ������
������![]() .
.

��1����̽��![]() ��
��![]() ��λ�ù�ϵ����֤����
��λ�ù�ϵ����֤����
��2����ͼ��2����![]() Ϊ
Ϊ![]() �ӳ���������һ��ʱ����1���еĽ����Ƿ��������˵�����ɣ�
�ӳ���������һ��ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ��3����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬
�ӳ�����һ�㣬![]() Ϊ
Ϊ![]() ��һ���㣬�ֱ���
��һ���㣬�ֱ���![]() Ϊ��������������
Ϊ��������������![]() �͵���������
�͵���������![]() ��ʹ��
��ʹ��![]() ������
������![]() .Ҫʹ��1���еĽ�����Ȼ����������Ҫ����������������Ϊʲô��
.Ҫʹ��1���еĽ�����Ȼ����������Ҫ����������������Ϊʲô��
���𰸡���1��![]() ������������2��������
������������2��������![]() ������������3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������
������������3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������![]() ��������.
��������.
��������
��1��ͨ���ȱ������ε����ʣ���������ȡ���������ȣ����PF=PC��PE=PQ����EPF=��QPC��Ȼ�����ȫ�������ε��ж�����SAS֤����PFE�ա�PCQ���ٸ���ȫ�������ε����ʣ���Ӧ����ȣ�֪��EPF=��QPC=90������������ƽ���ߵ��ж�������ͬλ����ȣ���ֱ��ƽ�У�֪PF��AB�������ƽ���ߵ����ʣ���ƽ�����У���һ����ֱ�ڵ�����ֱ�ߣ�����һ��Ҳ��ֱ�ڵ�����ֱ�ߣ�֪EF��AB��
��2��ͨ���ȱ������ε����ʣ���������ȡ���������ȣ����PF=PC��PE=PQ����EPF=��QPC��Ȼ�����ȫ�������ε��ж�����SAS֤����PFE�ա�PCQ���ٸ���ȫ�������ε����ʣ���Ӧ����ȣ�֪��EPF=��QPC=90������������ƽ���ߵ��ж��������ڴ�����ȣ���ֱ��ƽ�У�֪PF��AB�������ƽ���ߵ����ʣ���ƽ�����У���һ����ֱ�ڵ�����ֱ�ߣ�����һ��Ҳ��ֱ�ڵ�����ֱ�ߣ�֪EF��AB��
��3����Ҫ���ӵ����������㣺![]() ���ڴ�����ȣ���ֱ��ƽ�У���
���ڴ�����ȣ���ֱ��ƽ�У���
��1��![]() ��֤�����£�
��֤�����£�
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��![]() ��
��

��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��2��������![]() ���������£�
���������£�
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��

��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
��3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������![]() ���������£�
���������£�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������������3������4��0��+5����![]()
��1����Щ�������У��������� �������Ǹ������� ������
��2�������ᣬ���������ϱ�ʾ��Щ��������
��3���������������������������������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪһ�η��̽�Ӧ���⣺
ѧ�������ʽ������ؽ������ʵ���������ũ����ժ�˻ƹϺ����ӹ�80ǧ�ˣ��˽��Щ�߲˵���ֲ�ɱ���180Ԫ�����˽������Ϣ��
��1�����ժ�ĻƹϺ����Ӹ�����ǧ�ˣ�
��2����Щ��ժ�ĻƹϺ����ӿ�����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ���߳��ֱ�Ϊ
���߳��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������������ε������С��ͬѧ�������ʱ�Ȼ���һ��ÿ��С�����εı߳���Ϊ1���������������������л������
������������ε������С��ͬѧ�������ʱ�Ȼ���һ��ÿ��С�����εı߳���Ϊ1���������������������л������![]() ��
��![]() �������㶼������ĸ���ϣ�.��ͼ1��ʾ����������������
�������㶼������ĸ���ϣ�.��ͼ1��ʾ����������������![]() �ĸߣ�������������ε���������ַ����й��취.
�ĸߣ�������������ε���������ַ����й��취.
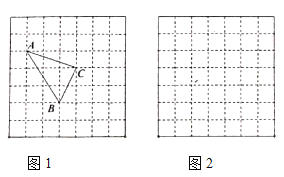
��1��![]() �����Ϊ___________________.
�����Ϊ___________________.
��2����![]() �����߳��ֱ�Ϊ
�����߳��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������ͼ2�������л���
������ͼ2�������л���![]() ��ʹ��
��ʹ��![]() ���������㶼�ڸ���ϣ���������ε����.
���������㶼�ڸ���ϣ���������ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������a,b,�������������������������������涨: a��b=a2+2ab,a��b=|a+ b|-|a- b|,���磬2��(- 1)=22+2��2��(-1)=0,(- 2) ��3=|-2+3|-| - 2-3|= -4.![]() b c
b c
(1)����(- 3) ��2��ֵ;
(2)��a, b�������ϵ�λ����ͼ��ʾ������a��b;
![]()
(3)��(-2) ��x=2��(- 4)+ 3x,��x��ֵ:
(4)��������������m,n,���㶨��һ�������������� ��ʹ��(-3) ��5 = 4,ֱ��д���㶨�������:m��n=_ (�ú�m,n��ʽ�ӱ�ʾ).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A,B��ֱ��1��,AB = 20cm,��BAC= 120��.

(1)��P��A������������AB��ÿ��2cm���ٶ������˶���ͬʱ��Q��B����,������BA��ÿ��lcm���ٶ������˶�,���P����������ʱ���Q�غ�?
(2)��(1)�������£����P����������ʱ���Q���5cm?
(3)��MΪ����AC��һ��,AM = 4cm,�ֽ�����AC�Ƶ�A��ÿ��30�����ٶ�˳ʱ����תһ�ܺ�ֹͣ��ͬʱ��N�ӵ�B������ֱ��AB�����˶�������һ�˶������У��Ƿ����ijһʱ�̣�ʹ�õ�NΪBM���е�?�����ڣ������N�˶����ٶ�:��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪C,D���߶�AB�ϵ������㣬M,N�ֱ�ΪAC,BD���е�.
![]()
��1����![]() ����
����![]() �ij���MN�ij���
�ij���MN�ij���
��2�����![]() ���ú�a,b��ʽ�ӱ�ʾMN�ij�.
���ú�a,b��ʽ�ӱ�ʾMN�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij���Բμ���ģ�⿼�Ե�8000��ѧ������ѧ�ɼ����г������飬��ȡ�˲���ѧ������ѧ�ɼ�������Ϊ����������ͳ�ƣ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ������ͼ����֪���������С���Ƶ����֮��������6��7��11��4��2������С���Ƶ����40��
��1�����ε��鹲��ȡ�˶�����ѧ����
��2����72�����ϣ���72�֣�Ϊ����96�����ϣ���96�֣�Ϊ���㣬��ô��ȡ��ѧ���У�����������������������ռ����ȡ��ѧ�����İٷ�֮���٣�
��3�����ݣ�2���Ľ��ۣ��������вμ���ģ�⿼�Ե�ѧ������������������������Լ�Ƕ����ˣ�
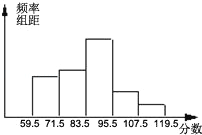
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2018��һ���Ĺ����ų���ͼ��ʾ��10�У��涨���ϵ�������Ϊ1�С�2�С�3����������������Ϊ��1������10�У�

��1����2018���� ������ ����
��2����ͼ�д���Ӱ��3�����൱��һ������ƽ�ƣ��豻��ס��3�����У�����һ����Ϊx��
����ס���������ĺͣ��ú�x��ʽ�ӱ�ʾ����
�ڱ���ס���������ĺ��ܷ���2017�����ܣ����x��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com