
【题目】![]() 三边长分别为
三边长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点
,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点![]() (
(![]() 各个顶点都在网格的格点上).如图1所示,这样借用网格(不需
各个顶点都在网格的格点上).如图1所示,这样借用网格(不需![]() 的高)就能算出三角形的面积,这种方法叫构造法.
的高)就能算出三角形的面积,这种方法叫构造法.
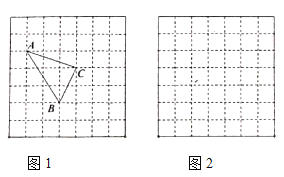
(1)![]() 的面积为___________________.
的面积为___________________.
(2)若![]() 的三边长分别为
的三边长分别为![]() 、
、![]() 、
、![]() ,请在图2的网格中画出
,请在图2的网格中画出![]() ,使得
,使得![]() 的三个顶点都在格点上,求此三角形的面积.
的三个顶点都在格点上,求此三角形的面积.
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解下列各题:
(1)先化简,再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:
(2)解方程:![]() =1-
=1-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用![]() 、
、![]() 表示,且
表示,且![]() .
.
(1)数轴上点A表示的数是 ,点B表示的数是
(2)若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;动点Q从原点O出发,以1个单位长度/秒速度向B运动,点P、Q同时出发,点Q运动到B点时两点同时停止.设点Q运动时间为t秒.
①若P从A到B运动,则P点表示的数为 ,Q点表示的数为 .用含![]() 的式子表示)
的式子表示)
②当t为何值时,点P与点Q之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()

(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上任意一点,
边上任意一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() .
.

(1)试探索![]() 与
与![]() 的位置关系,并证明;
的位置关系,并证明;
(2)如图(2)当![]() 为
为![]() 延长线上任意一点时,(1)中的结论是否成立?请说明理由;
延长线上任意一点时,(1)中的结论是否成立?请说明理由;
(3)如图(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等腰三角形
为边作等腰三角形![]() 和等腰三角形
和等腰三角形![]() ,使得
,使得![]() ,连接
,连接![]() .要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
.要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解长沙市七年级学生身体素质,从全市七年级学生中随机抽取部分学生进行了一次体育考试科目的测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试记录绘成如下两幅完全不同的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生数是________;
(2)图1中![]() 的度数是________;把图2条形统计图补充完成;
的度数是________;把图2条形统计图补充完成;
(3)长沙市某区七年级共有9800名学生,如果全部参加这次体育科目测试,请估计不及格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
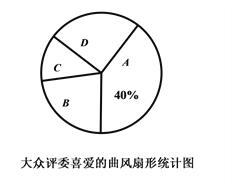
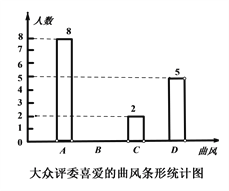
【题目】春雨初歇,绿意葱茏,重庆南开(融侨)中学初2020级举行了“春天的赞礼”为主题的合唱比赛,各班演唱歌曲的曲风有:青春舞曲、经典名曲、动漫神曲、励志金曲四种类型,为了了解同学们对各种曲风的喜爱程度。校学生处对大众评委喜爱的歌曲曲风进行了调查,(A—喜爱青春舞曲、B—喜爱经典名曲、C—喜爱动漫神曲、D—喜爱励志金曲),先根据调查得到如下图不完整的统计图,请结合图中信息完成下列问题:
![]() 扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
![]() 在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com