
【题目】先让我们一起来学习方程m2+1= ![]() 的解法:
的解法:
解:令m2=a,则a+1= ![]() ,方程两边平方可得,(a+1)2=a+3
,方程两边平方可得,(a+1)2=a+3
解得a1=1,a2=﹣2,∵m2≥0∴m2=1∴m=±1
点评:类似的方程可以用“整体换元”的思想解决.
不妨一试:
如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式;
(2)①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);
(3)当△PHO为等边三角形时,求点P坐标;
(4)如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+1经过点A(4,﹣3),
∴﹣3=16a+1,
∴a=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+1,顶点B(0,1)
x2+1,顶点B(0,1)
(2)=
②当P点在抛物线上运动时,猜想PO与PH有何数量关系,并证明你的猜想;
解:结论:PO=PH.理由:设点P坐标(m,﹣ ![]() m2+1),
m2+1),
∵PH=2﹣(﹣ ![]() m2+1)=
m2+1)= ![]() m2+1PO=
m2+1PO= ![]() =
= ![]() m2+1,
m2+1,
∴PO=PH
(3)
解:∵△PHO为等边三角,
∴OP=OH.
由两点间的距离公式可知:OH= ![]() .
.
∴ ![]() m2+1=
m2+1= ![]() ,解得:m=±2
,解得:m=±2 ![]() ,
,
∴P(2 ![]() ,﹣2)、(﹣2
,﹣2)、(﹣2 ![]() ,﹣2)
,﹣2)
(4)
解:∵BC= ![]() =
= ![]() ,AC=
,AC= ![]() =
= ![]() ,AB=
,AB= ![]() =4
=4 ![]() .
.
∴BC=AC,
∵PO=PH,以P,O,H为顶点的三角形与△ABC相似,
∴PH与BC,PO与AC是对应边,
∴ ![]() ,设点P(m,﹣
,设点P(m,﹣ ![]() m2+1),
m2+1),
∴ ![]() =
= ![]() ,解得m=±1.
,解得m=±1.
∴点P坐标(1, ![]() )或(﹣1,
)或(﹣1, ![]() )
)
【解析】解: (2)①当P点运动到A点处时.
∵PO=5,PH=5,
∴PO=PH.
所以答案是:=.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个有理数a,b,c,已知a=![]() ,(n为正整数)且a与b互为相反数,b与c互为倒数.
,(n为正整数)且a与b互为相反数,b与c互为倒数.
(1)当n为奇数时你能求出a,b,c各是几吗?
(2)当n为偶数时,你能求a,b,c三数吗?若能请算出结果,不能请说明理由.
(3)根据(1)中的结论,求:ab﹣b﹣(b﹣c)2015的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=4 ![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
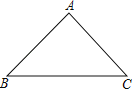
【题目】如图,已知△ABC
(1)用直尺和圆规作△ABC的边BC上的高AD,并在线段AD上找一点E,使E到AB的距离等于ED(不写作法,保留作图痕迹);
(2)若AB=AC=5,BC=6,求出ED的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com