
【题目】有三个有理数a,b,c,已知a=![]() ,(n为正整数)且a与b互为相反数,b与c互为倒数.
,(n为正整数)且a与b互为相反数,b与c互为倒数.
(1)当n为奇数时你能求出a,b,c各是几吗?
(2)当n为偶数时,你能求a,b,c三数吗?若能请算出结果,不能请说明理由.
(3)根据(1)中的结论,求:ab﹣b﹣(b﹣c)2015的值.
【答案】(1)a=2, b=﹣2,c=﹣![]() ;(2)a=-2, b=2,c=
;(2)a=-2, b=2,c=![]() ;(3) ﹣4+2n+(
;(3) ﹣4+2n+(![]() )2015.
)2015.
【解析】
(1)当n为奇数时,先求出a,再根据相反数和倒数的定义可求b,c各是几;
(2)当n为偶数时,先求出a,再根据相反数和倒数的定义可求b,c各是几;
(3)根据(1)中的结论代入计算即可求解.
解:(1)当n为奇数时,a=![]() =2,
=2,
∵a与b互为相反数,b与c互为倒数,
∴b=﹣2,c=﹣![]() ;
;
(2)当n为偶数时,a=![]() =﹣2,
=﹣2,
∵a与b互为相反数,b与c互为倒数,
∴b=2,c=![]() ;
;
(3)∵a=2,b=﹣2,c=﹣![]() ,
,
∵ab﹣bn﹣(b﹣c)2015=2×(﹣2)+2n﹣(﹣2+![]() )2015=﹣4+2n+(
)2015=﹣4+2n+(![]() )2015.
)2015.


科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
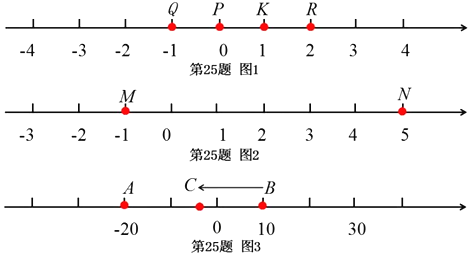
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:
的好点.同理可以判断:
点P__________有序点对![]() 的好点,点R______________有序点对
的好点,点R______________有序点对![]() 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对![]() 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期天下午,小强和小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程![]() (公里)和所用时间
(公里)和所用时间![]() (分钟)之间的函数关系.下列说法中错误的是( )
(分钟)之间的函数关系.下列说法中错误的是( )
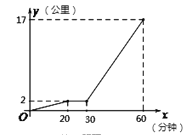
A. 小强从家到公共汽车站步行了2公里 B. 小强在公共汽车站等小明用了10分钟
C. 小强乘公共汽车用了20分钟 D. 公共汽车的平均速度是30公里/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先让我们一起来学习方程m2+1= ![]() 的解法:
的解法:
解:令m2=a,则a+1= ![]() ,方程两边平方可得,(a+1)2=a+3
,方程两边平方可得,(a+1)2=a+3
解得a1=1,a2=﹣2,∵m2≥0∴m2=1∴m=±1
点评:类似的方程可以用“整体换元”的思想解决.
不妨一试:
如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式;
(2)①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);
(3)当△PHO为等边三角形时,求点P坐标;
(4)如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com