
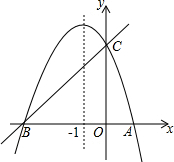
 ��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���������߾���A��1��0����C��0��3�����㣬��x�ύ��A��B���㣮
��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���������߾���A��1��0����C��0��3�����㣬��x�ύ��A��B���㣮���� ��1������A��B����x=-1�ԳƼ������B�����꣬Ȼ�����ô���ϵ����������������ߵĽ���ʽ��
��2�����BC��Գ���Ľ������M��
��3����P�������ǣ�-1��p������������֮��ľ��빫ʽ��ʾ��BC��BP��PC�ij���Ȼ��ֳɡ�BPC�����߷ֱ���б������������ۣ����ù��ɶ����з������p��ֵ���õ�P�����꣮
��� �⣺��1��A��1��0������x=-1�ĶԳƵ��ǣ�-3��0������B�������ǣ�-3��0����
��������ã�$\left\{\begin{array}{l}{-3m+n=0}\\{n=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$��
�������ߵĽ���ʽ��y=x+3��
��������ã�$\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽ��y=-x2-2x+3��
��2����y=x+3����x=-1����y=-1+3=2��
��M�������ǣ�-1��2����
��3����P�������ǣ�-1��p����
��BP2=��-1+3��2+p2=4+p2��
PC=��0+1��2+��3-p��2=p2-6p+10��
BC=32+32=18��
��BCʱб��ʱ��BP2+PC2=BC2����4+p2��+��p2-6p+10��=18��
��ã�p=-1��2��
��P�������ǣ�-1��-1����-1��2����
��BP��б��ʱ��BP2=PC2+BC2����4+p2=��p2-6p+10��+18��
��ã�p=4��
��P�������ǣ�-1��4����
��PC��б��ʱ��PC2=BP2+BC2����p2-6p+10=4+p2+18��
��ã�p=-2��
��P�������ǣ�-1��-2����
��֮��P�������ǣ�-1��-1����-1��2����-1��4����-1��-2����
���� ���⿼���˴���ϵ���������Ľ���ʽ���Լ��ԳƵ����ʺ��ɶ�������ȷ����p��ʾ����BPC�ı�BP��PC�ij��ǹؼ���


 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+5 | B�� | x-5 | C�� | x2-25 | D�� | �����ϴ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | һ | �� | �� | �� | �� |
| ÿ���ǵ� | +1 | +1.5 | -1.5 | -2.5 | +0.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Ϊ�˹��Ƴ�������A��B�����ľ��룬С�hͬѧ�ڳ���һ��ѡȡһ��O�����OA=12�ף�OB=7�ף���A��B��ľ��벻�����ǣ�������
��ͼ��Ϊ�˹��Ƴ�������A��B�����ľ��룬С�hͬѧ�ڳ���һ��ѡȡһ��O�����OA=12�ף�OB=7�ף���A��B��ľ��벻�����ǣ�������| A�� | 5�� | B�� | 7�� | C�� | 10�� | D�� | 18�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com