
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为![]() 万元,可变成本逐年增长,已知该养殖户第
万元,可变成本逐年增长,已知该养殖户第![]() 年的可变成本为
年的可变成本为![]() 万元,第
万元,第![]() 年的养殖成本为
年的养殖成本为![]() 万元,现在要求可变成本平均每年增长的百分率,我们可设可变成本平均的每年增长的百分率为
万元,现在要求可变成本平均每年增长的百分率,我们可设可变成本平均的每年增长的百分率为![]() ,则可列方程为________.
,则可列方程为________.
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛(满分100分),如下表所示:
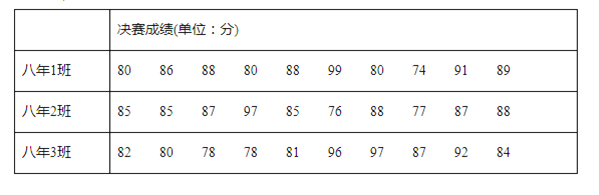
解答下列问题:
(1)请填写下表:
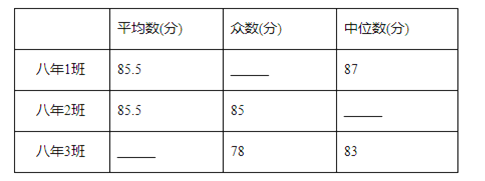
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好);
②从平均数和中位数相结合看(分析哪个班级成绩好);
(3)如果在每个班级参加决赛的选手中选出3人参加总决赛,你认为哪个班级的实力更强一些,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分别是以A1,A2,A3,…An…为直角顶点的等腰直角三角形,则△B10A10A11的面积是________.
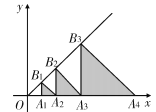
查看答案和解析>>
科目:初中数学 来源: 题型:
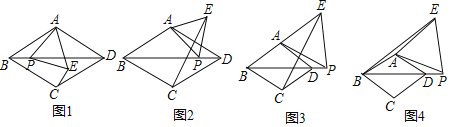
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随点P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是_________,CE与AD的位置关系是____________________;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3)如图4,当点P在线段BD的延长线上时,连接BE,若![]() ,求四边形ADPE的面积.
,求四边形ADPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某中学对学生会倡导的“献爱心”捐款活动进行抽样调查,被调查的学生捐款情况如图所示。
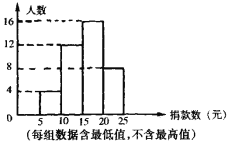
(1)该校共调查了______名学生。
(2)捐款15元以上的学生频率是_______。
(3)若该校共有1800名学生,估计全校学生一共捐款至少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
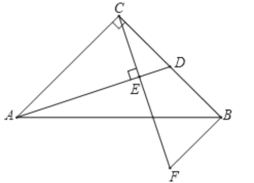
【题目】如图所示,在△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F.
(1)求证:AC=2BF
(2)连接DF,求证:AB垂直平分DF
(3)连接AF,试判断△ACF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=![]() ∠BAD,若DF=1,BE=5,则线段EF的长为( )
∠BAD,若DF=1,BE=5,则线段EF的长为( )
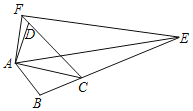
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com