
【题目】在平面直角坐标中,A (0,5)、B (4,0)、C (2,5),四边形AOBC经过平移后得到四边形A′O′B′C′.

(1) 如图1,若A′(-3,5),四边形AOBC内部一点M(a+b-2,6a-7)经过平移后得到点N(a+2b-7,4b-6),求M点的坐标
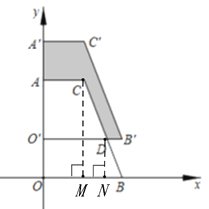
(2) 如图2,若四边形AOBC向右平移m个单位长度(m>0).当m为何值时,重叠部分的面积比四边形BB′C′C的面积大
(3) 如图3,若四边形AOBC向上平移2个单位长度,直接写出图中阴影部分的面积.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,重叠部分的面积比四边形BB′C′C的面积大;(3)
时,重叠部分的面积比四边形BB′C′C的面积大;(3)![]()
【解析】
(1)根据对应点的横坐标和纵坐标的变化确定平移方向和平移距离;
(2)用m表示线段长,根据梯形面积公式表示出重叠部分和四边形BB′C′C的面积,根据二者的关系列出不等式求解;
(3)根据平移性质和勾股定理求出OD的长度,由图形特征得出阴影部分的面积等于梯形OBDO的面积,根据梯形面积公式计算.
(1)∵A (0,5),A′(-3,5),
∴四边形AOBC向左平移3个单位得到四边形A′O′B′C′,
∵M(a+b-2,6a-7)对应点为N(a+2b-7,4b-6),
∴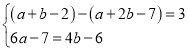 ,
,
∴![]() ,
,
∴M点的坐标为:![]() .
.
(2)∵A (0,5)、B (4,0)、C (2,5),
∴AO=5,AC=2,OB=4,
根据题意得,![]() ,
,
解得,![]() ,
,
∴![]() .
.
∴当![]() 时,重叠部分的面积比四边形BB′C′C的面积大.
时,重叠部分的面积比四边形BB′C′C的面积大.
(3)如图,由图形可得,阴影部分的面积等于梯形OBDO的面积,
过C作CM⊥x轴于M点,作DN⊥x轴于N点,
∴∠OND=∠NDO=∠OON=90°,
∴四边形ONDO是矩形,∴ON=OD,OO=ND=2
∵∠AOM=∠OMC=∠OAC=90°,
∴四边形OMCA是矩形,
∴CM=OA=5,AC=OM=2
∴BM=OB-OM=4-2=2,
在Rt△CMB中,由勾股定理得BC=![]() ,
,
∵AC∥OD∥OB,
∴![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
在Rt△DNB中,由勾股定理得,BN=![]() ,
,
∴ON=OB-BN=4-![]() =
=![]() ,
,
∴ON=OD=![]() ,
,
∴S梯形OBDO=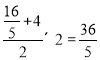 .
.
即阴影部分的面积为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式.并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多20%,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
查看答案和解析>>
科目:初中数学 来源: 题型:
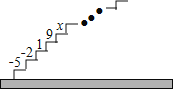
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 y =kx2 +(k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.

认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知y=(m2+m)![]() +(m﹣3)x+m2是x的二次函数,求出它的解析式.
+(m﹣3)x+m2是x的二次函数,求出它的解析式.
(2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校随机选取40名学生进行军运会知识考查,对考查成绩进行统计(成绩均为整数),并依据统计数据绘制了如下统计图表.解答下列问题:
组别 | 分数段/分 | 频数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |

(1) 表中a=______;b=______;c=____;
(2) 请补全频数分布直方图;
(3) 已知该学校共有学生1280人,若考查成绩80分以上(不含80分)为优秀,试估计该学校学生军运会知识考查成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
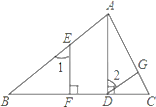
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
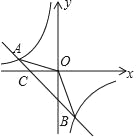
【题目】(8分)已知A(﹣4,m+10)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com