
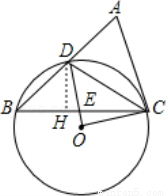
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
(1)求证:直线AC是⊙O的切线;
(2)如果∠ACB=75°.
①若⊙O的半径为2,求BD的长;
②求CD:BC的值.

(1)证明见解析;(2)①BD=2;②CD:BC的值为 ﹣1.
﹣1.
【解析】
试题分析:(1)由∠DOC=2∠ACD=90°易得∠ACD=45°,而OC=OD,则可判断△OCD为等腰直角三角形,所以∠OCD=45°,则∠OCA=90°,于是可根据切线的判定定理得到直线AC是⊙O的切线;
(2)作DH⊥BC于H.
①先根据等腰直角三角形的性质得CD=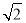 OC=2
OC=2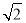 ,再根据圆周角定理得∠B=
,再根据圆周角定理得∠B=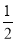 ∠COD=∠B=45°,由于∠ACB=75°,∠ACD=45°,所以∠BCD=30°;在Rt△CDH中,根据含30度的直角三角形三边的关系得DH=
∠COD=∠B=45°,由于∠ACB=75°,∠ACD=45°,所以∠BCD=30°;在Rt△CDH中,根据含30度的直角三角形三边的关系得DH=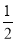 DC=
DC=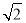 ,在Rt△BDH中,根据等腰直角三角形的性质得BD=
,在Rt△BDH中,根据等腰直角三角形的性质得BD=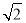 DH=2;
DH=2;
②设DH=x,在Rt△CDH中,根据含30度的直角三角形三边的关系得到CD=2DH=2x,CH= DH=
DH= x;在Rt△BDH中,根据等腰直角三角形的性质得BH=DH=x,则BC=(
x;在Rt△BDH中,根据等腰直角三角形的性质得BH=DH=x,则BC=( +1)x,所以CD:BC=2x:(
+1)x,所以CD:BC=2x:( +1)x=(
+1)x=( ﹣1):1.
﹣1):1.
试题解析:(1)∵∠DOC=2∠ACD=90°,
∴∠ACD=45°,
∵OC=OD,
∴△OCD为等腰直角三角形,
∴∠OCD=45°,
∴∠OCA=∠OCD+∠ACD=90°,
∴OC⊥AC,
∴直线AC是⊙O的切线;
(2)作DH⊥BC于H,如图,
①在Rt△OCD中,CD=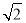 OC=2
OC=2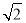 ,
,
∵∠B=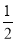 ∠COD,
∠COD,
∴∠B=45°,
∵∠ACB=75°,∠ACD=45°,
∴∠BCD=30°,
在Rt△CDH中,DH=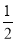 DC=
DC=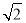 ,
,
在Rt△BDH中,BD=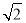 DH=
DH=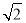 ×
×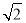 =2;
=2;
②设DH=x,
在Rt△CDH中,CD=2DH=2x,CH= DH=
DH= x,
x,
在Rt△BDH中,BH=DH=x,
∴BC=BH+CH=x+ x=(
x=( +1)x,
+1)x,
∴CD:BC=2x:( +1)x=(
+1)x=( ﹣1):1,即
﹣1):1,即
CD:BC的值为 ﹣1.
﹣1.
考点:1.切线的判定2.相似三角形的判定与性质.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:解答题
已知直线 与x轴、y轴分别交于B点、A点,直线
与x轴、y轴分别交于B点、A点,直线 与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。
与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:选择题
下列计算正确的是
A.3x2·4x2=12x2 B.x3·x5=x15 C.x4÷x=x3 D.(x5)2=x7
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:选择题
如图,平行四边形ABCD中,CE⊥AB于E,若∠A=125°,则∠BCE的度数为( )

A.35° B.55° C.25° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com