
分析 利用非负整数,正分数,以及无理数的定义判断即可.
解答 解:非负整数集合:{(-2)2、0、-(-11),…}
正分数集合:{$\frac{22}{7}$、15%,0.$\stackrel{•}{3}$、|-2$\frac{3}{5}$|,…}
无理数集合:{$\frac{2}{π}$、10.01001000100001…,…}.
故答案为:(-2)2、0、-(-11),;$\frac{22}{7}$、15%,0.$\stackrel{•}{3}$、|-2$\frac{3}{5}$|,;$\frac{2}{π}$、10.01001000100001…,
点评 此题考查了实数,熟练掌握各自的定义是解本题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
 如图,长方形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).长方形O'A'BC'是长方形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上,O'C'交AB于点D.
如图,长方形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).长方形O'A'BC'是长方形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上,O'C'交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
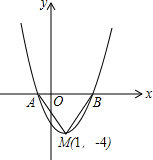 如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com