
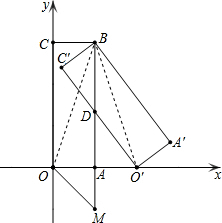
 ��ͼ��������OABC�ı�OA��x���������ϣ���OC��y���������ϣ�B�������Ϊ��1��3����������O'A'BC'�dz�����OABC��B����ʱ����ת�õ��ģ�O'��ǡ����x����������ϣ�O'C'��AB�ڵ�D��
��ͼ��������OABC�ı�OA��x���������ϣ���OC��y���������ϣ�B�������Ϊ��1��3����������O'A'BC'�dz�����OABC��B����ʱ����ת�õ��ģ�O'��ǡ����x����������ϣ�O'C'��AB�ڵ�D������ ��1������OB��O��B��������ת�����ʿɵ�OB=O��B���ٸ��ݾ��ε�����BA��OA���ٸ��ݵ������������ߺ�һ�����ʿɵ�AO=AO�䣬Ȼ����ݵ�B���������AO�ij��ȣ��ٵõ�AO��ij��ȣ���O������꼴�ɵõ���
��2�����D�������ǣ�1��a������ʾ��O��D�ij��ȣ�Ȼ�����ù��ɶ�����ʽ���a��ֵ���Ӷ��õ���D�����꣬�ٸ��ݴ���ϵ������ʽ�������ֱ��C��O��Ľ���ʽ��
��3������AM=1�ɵá�AOM�ǵ���ֱ�������Σ�Ȼ��֢�PM����һֱ�DZߣ���PMA=45�㣬��PO����һֱ�DZߣ���POA=45�����������ʽ���м��㼴�ɵý⣮
��� �⣺ ��1����ͼ������OB��O��B����OB=O��B��
��1����ͼ������OB��O��B����OB=O��B��
���ı���OABC�Ǿ��Σ�
��BA��OA��
��AO=AO�䣬
��B���������1��3����
��OA=1��
��AO��=1��
���O��������ǣ�2��0����
��2�����D��������1��a������AD=a��
�ߵ�B�������ǣ�1��3����
��O��D=3-a��
��Rt��ADO����AD2+AO��2=O��D2��
��a2+12=��3-a��2��
���a=$\frac{4}{3}$��
���D��������1��$\frac{4}{3}$����
��ֱ��C��O��Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{2k+b=0}\\{k+b=\frac{4}{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{8}{3}}\end{array}\right.$��
���C��O������ֱ�ߵĽ���ʽ��y=-$\frac{4}{3}$x+$\frac{8}{3}$��
��3����AM=1��AO=1����AM��AO��
���AOM�ǵ���ֱ�������Σ�
��PM����һֱ�DZ�ʱ����PMA=45�㣬
��PA=AM=1����P���O���غϣ�
���P�������ǣ�2��0����
��PO����һֱ�DZߣ���POA=45�㣬��PO���ڵ�ֱ��Ϊy=x��
��$\left\{\begin{array}{l}{y=-\frac{4}{3}x+\frac{8}{3}}\\{y=x}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{8}{7}}\\{y=\frac{8}{7}}\end{array}\right.$��
���P������ΪP��2��0����$\frac{8}{7}$��$\frac{8}{7}$����
���� �����Ƕ��ı��ε��ۺϿ��飬��Ҫ�о��ε����ʣ��������������ߺ�һ�����ʣ�ȫ�������ε��ж������ʣ�����ϵ������������ʽ�����ɶ����ȣ��ۺ��Խ�ǿ���Ѷ��еȣ�����ϸ����ϸ�ļ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪һ�κ���y=kx+b��ͼ����ͼ��ʾ��
��֪һ�κ���y=kx+b��ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
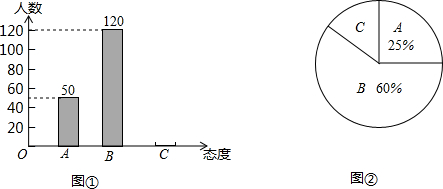
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ABN�͡�ACMλ����ͼ��ʾ��AB=AC����1=��2����M=��N����֤��AD=AE��
��֪��ABN�͡�ACMλ����ͼ��ʾ��AB=AC����1=��2����M=��N����֤��AD=AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com