练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知△ABN和△ACM位置如图所示，AB=AC，∠1=∠2，∠M=∠N．求证：AD=AE．

    分析 先证明∠BDA=∠CEA，由SAS证明△ABD≌△ACE，得出对应边相等即可．

    解答 证明：
    ∵∠M=∠N，
    ∴∠MDO=∠NEO，
    ∴∠BDA=∠CEA，
    ∴在△ABD和△ACE中，
    ∵$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{∠BDA=∠CEA}\end{array}\right.$，
    ∴△ABD≌△ACE（AAS），
    ∴AD=AE．

    点评 本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

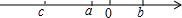    12．实数a、b、c在数轴上的位置如图所示，则$\sqrt{（a-b）^{2}}$-|a+c|+$\sqrt{（c-b）^{2}}$-|-b|=b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．“十•一”期间，我市某生态公园在7天中每天游客的人数变化如表（正数表示比前一天多的人数，负数表示比前一天少的人数）
    日期10月1日10月2日10月3日10月4日10月5日10月6日10月7日
    人数变化
    单位：万人    		+1.6+0.8+0.4-0.4-0.8+0.2-1.2
    （1）若9月30日的游客人数记为a万人，请用含有a的式子表示10月2日的游客人数？
    （2）请判断七天内游客人数最多的是哪天？请说明理由．
    （3）建生态公园的目的一般有两个，一方面是给广大市民提供一个休闲游玩的好去处；另一方面是拉动内需，促进消费．若9月30日的游客人数为1万人，进园的人每人平均消费100元．问“十•一”期间所有的游园人员在生态园的总消费是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（π-3.14）0-|-5|+（$\frac{1}{3}$）-2+（-1）2013
    （2）2（a4）3-a2a10+（-2a5）2÷a2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，长方形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为（1，3）．长方形O'A'BC'是长方形OABC绕B点逆时针旋转得到的．O'点恰好在x轴的正半轴上，O'C'交AB于点D．
    （1）求证：O'A=O'A'，并求点O'的坐标．（提示：连接BO、BO'）
    （2）求边C'O'所在直线的解析式．
    （3）延长BA到M使AM=1，在（2）中求得的直线上是否存在点P，使得△POM是以线段OM为直角边的直角三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知：如图，点E、F在AD上，且AF=DE，∠B=∠C，AB∥DC．求证：AB=DC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

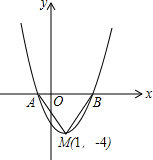    14．如图是二次函数y=（x-1）2-4的图象，与x轴交于A，B两点．将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b（b＜1）与此图象有两个公共点时，b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某商场将进货单价为100元的某种商品按零售价130元一个售出时，每星期能卖出80个，商家决定降价促销，根据市场调查，每件商品每降低1元，每星期可多卖4件．
    （1）求商家降价前每星期的利润是多少？
    （2）设每件商品降价x元，降价后每星期的利润为y元，求y与x的函数关系式．
    （3）商家要使每星期的销售利润最大，应将售价定为每件多少元？每星期的最大销售利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，抛物线y=x2+bx+c与x轴交A（-1、0）、B（3，0）两点，与y轴交于点C，顶点为D．
    （1）求抛物线的解析式；
    （2）抛物线上有一动点M，在抛物线的对称轴上是否存在一点N，使以A，B，M，N为顶点的四边形是平行四边形，若存在直接写出M点的坐标．

    查看答案和解析>>

    同步练习册答案