
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
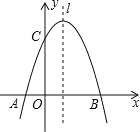
【答案】(1)m=2 ;(1,4);(2) (1,2).
【解析】
试题分析:(1)首先把点B的坐标为(3,0)代入抛物线y=![]() +mx+3,利用待定系数法即可求得m的值,继而求得抛物线的顶点坐标;
+mx+3,利用待定系数法即可求得m的值,继而求得抛物线的顶点坐标;
(2)首先连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,然后利用待定系数法求得直线BC的解析式,继而求得答案.
试题解析:(1)把点B的坐标为(3,0)代入抛物线y=![]() +mx+3得:0=
+mx+3得:0=![]() +3m+3,
+3m+3,
解得:m=2,
∴y=![]() +2x+3=
+2x+3=![]() ,
,
∴顶点坐标为:(1,4).
(2)连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,
设直线BC的解析式为:y=kx+b,
∵点C(0,3),点B(3,0),
∴![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为:y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴当PA+PC的值最小时,点P的坐标为:(1,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,求∠E1D1B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆小货车为一家汽车配件批发部送货,先向南走了8千米到达“小岗”修理部,又向北走了4.5千米到达“明城”修理部,继续向北走了6.5千米到达“中都”修理部,最后又回到批发部.
(1)请以批发部为原点,向南为正方向,用1个单位长度表示1千米,在数轴上表示出“小岗”“明城”“中都”三家修理部的位置;
(2)“中都”修理部距“小岗”修理部有多远?
(3)小货车一共行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列根据等式的性质正确变形的是( ).
A.由- ![]() x=
x= ![]() y,得x=2y
y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-5=7,得3x=7-5
查看答案和解析>>
科目:初中数学 来源: 题型:
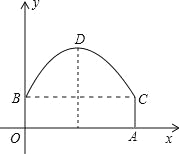
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系
(1)求该抛物线的解析式.
(2)一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
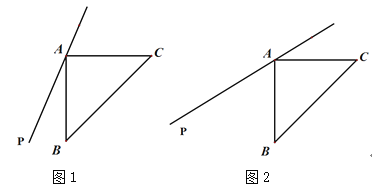
【题目】在等腰直角三角形ABC左侧作直线AP,点B关于直线AP的对称点为D,连结BD、CD,其中CD交直线AP于点E.
(1)依题意补全图1;
(2)若∠PAB=28°,求∠ACD的度数;
(3)如图2,若45°<∠PAB <90°,用等式表示线段AB,CE,DE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com