
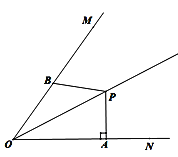
【题目】如图,P为∠MON平分线上一点,且OP=![]() ,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=
,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=![]() ,则OB=______.
,则OB=______.
【答案】2+![]() 或2-
或2- ![]()
【解析】过点P作PC⊥OM,然后分两种情况讨论:
如图1, 过点P作PC⊥OM,
因为P为∠MON平分线上一点,PA⊥ON,
所以PA=PC=1,
在Rt△OPC中,由勾股定理可得:
OC=![]() ,
,
在Rt△BPC中,由勾股定理可得:
BC=![]() ,
,
所以OB= OC-BC=2-![]() ,
,
如图2, 过点P作PC⊥OM,
因为P为∠MON平分线上一点,PA⊥ON,
所以PA=PC=1,
在Rt△OPC中,由勾股定理可得:
OC=![]() ,
,
在Rt△BPC中,由勾股定理可得:
BC=![]() ,
,
所以OB= OC+BC=2+![]() ,
,
故答案为: 2+![]() 或2-
或2-![]() .
.


点睛:本题主要考查角平分线的性质和勾股定理,解决本题关键是要分情况讨论进行求解.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】我们把符号“n!”读作“n的阶乘”,规定“其中n为自然数,当n≠0时,n!=n(n﹣1)(n﹣2)…21,当n=0时,0!=1”.例如:6!=6×5×4×3×2×1=720.
又规定“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加碱,有括号就先算括号里面的”.
按照以上的定义和运算顺序,计算:
(1)4!
(2)![]() ;
;
(3)(3+2)!﹣4!;
(4)用具体数试验一下,看看等式(m+n)!=m!+n!是否成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
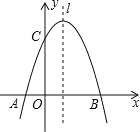
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com