
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,2)、(4,0),点P是直线y=2x+2上的一动点,当以P为圆心,PO为半径的圆与△AOB的一条边所在直线相切时,点P的坐标为__________.

【答案】(0,2),(﹣1,0),(﹣![]() ,1).
,1).
【解析】
先求出点C的坐标,分为三种情况:圆P与边AO相切时,当圆P与边AB相切时,当圆P与边BO相切时,求出对应的P点即可.
∵点A、B的坐标分别是(0,2)、(4,0),
∴直线AB的解析式为y=-![]() x+2,
x+2,
∵点P是直线y=2x+2上的一动点,
∴两直线互相垂直,即PA⊥AB,且C(-1,0),
当圆P与边AB相切时,PA=PO,
∴PA=PC,即P为AC的中点,
∴P(-![]() ,1);
,1);
当圆P与边AO相切时,PO⊥AO,即P点在x轴上,
∴P点与C重合,坐标为(-1,0);
当圆P与边BO相切时,PO⊥BO,即P点在y轴上,
∴P点与A重合,坐标为(0,2);
故符合条件的P点坐标为(0,2),(-1,0),(-![]() ,1),
,1),
故答案为(0,2),(-1,0),(-![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(a,0),B(0,b)且a,b满足![]() ,
,
点P在线段AB上(含端点)的一点,连接OP。
(1)若AB=![]() ,且△OBP是以OB为腰长的等腰三角形,求BP的长;
,且△OBP是以OB为腰长的等腰三角形,求BP的长;
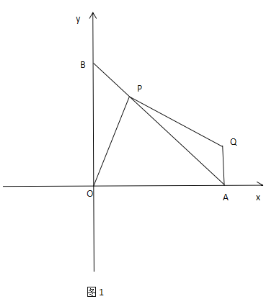
(2)如图1,过点A作AQ⊥x轴(Q在x轴上方),且满足∠OPQ=90°,求证:OP=PQ;
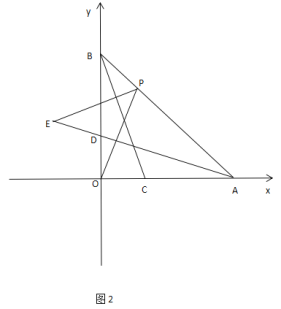
(3)如图2,C,D分别为OA,OB上的两点,且OC=OD,点P满足OP⊥AD,过点P作
PE⊥BC交AD的延长线于点E,试探究AE,OP,PE之间的数量关系,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.
(1)求证:△PAM≌△PFN;
(2)若PA=3,求AM+AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.

(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校位于小亮家北偏东35方向,距离为300m,学校位于大刚家南偏东85°方向,距离也为300m,则大刚家相对于小亮家的位置是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y= ax2+bx+c经过A(1,4)、B(-1,0)、C(-2,5)三点
(1)求抛物线的解析式并画出这条抛物线;
(2)直角坐标系中点的横坐标与纵坐标均为整数的点称为整点。试结合图象,写出在第四象限内抛物线上的所有整点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,重庆市南岸区广阳镇一果农李灿收获枇杷20吨,桃子12吨,现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.李灿安排甲、乙两种货车一次性地将水果运到销售地的方案数有( )
A.1种B.2种C.3种D.4种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com