
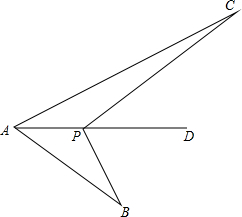
 已知点P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB.
已知点P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB. 分析 在AC上取AE=AB,然后证明△AEP≌△ABP,根据全等三角形对应边相等得到PB=PE,再根据三角形的任意两边之差小于第三边证明即可.
解答 证明:如图,在AC上截取AE,使AE=AB,连接PE,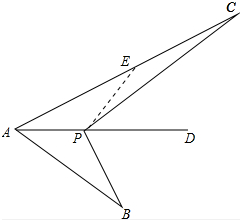
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
在△AEP和△ABP中,
$\left\{\begin{array}{l}{AE=AB}&{\;}\\{∠CAD=∠BAD}&{\;}\\{AP=AP}&{\;}\end{array}\right.$,
∴△AEP≌△ABP(SAS),
∴PE=PB,
在△PCE中,PC-PE<CE,
∴PC-PE<AC-AE,
∴PC-PB<AC-AB.
点评 本题主要考查了全等三角形的判定与性质、三角形的三边关系;通过作辅助线构造全等三角形是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
 已知正比例函数y=kx的图象经过点(3,-6).
已知正比例函数y=kx的图象经过点(3,-6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
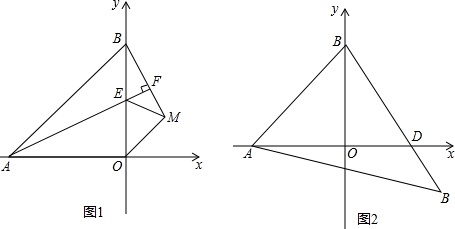
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
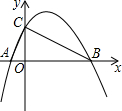 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com