练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长为（ ）

    A.4B.5C.6D.8

    【答案】A

    【解析】

    求出利用等腰三角形性质得到，AD=BD，根据∠FBD+∠C=90°，∠CAD+∠C=90°，推出∠FBD=∠CAD，根据ASA证△FBD≌△CAD，推出CD=DF即可．

    解：∵AD是△ABC的高，
    ∴AD⊥BC，
    ∴∠ADB=∠ADC=90°，
    ∵∠ABC=45°，
    ∴∠BAD=45°=∠ABD，
    ∴AD=BD，
    ∵BE⊥AC，
    ∴∠BEC=90°，
    ∴∠FBD+∠C=90°，∠CAD+∠C=90°，
    ∴∠FBD=∠CAD，
    在△FBD和△CAD中
    ，
    ∴△FBD≌△CAD（ASA），
    ∴CD=DF=4，
    所以选A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】义安中学工会“三八妇女节”共筹集会费1800元，工会决定拿出不少于270元，但不超过300元的资金为“优秀女职工”购买纪念品，其余的钱用于给50位女职工每人买一瓶洗发液或护发素，已知每瓶洗发液比每瓶护发素贵9元，用200元恰好可以买到2瓶洗发液和5瓶护发素．

    （1）求每瓶洗发液和每瓶护发素价格各是多少元？

    （2）有几种购买洗发液和护发素的方案？哪种方案用于为“优秀女职工”购买纪念品的资金更充足？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八(1)班组织了一次食品安全知识竞赛，甲、乙两队各5人的成绩如表所示(10分制)．

    数据

    中位数

    众数

    方差

    甲

    8

    10

    9

    6

    9

    9

    1.84

    乙

    10

    8

    9

    7

    8

    8

    1.04

    (1)补全表格中的众数和中位数

    (2)并判断哪队的成绩更稳定？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中的位置如图所示．

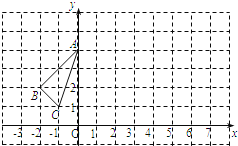
    （1）画出△ABC关于y轴对称的△A1B1C1；

    （2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；

    （3）观察△A1B1C1和△A2B2C2，它们是否关于某条直线对称？若是，请在图上画出这条对称轴．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等边三角形ABC的边长为7，点D为AB上一点，点E在BC的延长线上，且CE=AD，连接DE交AC于点F，作DH⊥AC于点H，则线段HF的长为 ____________.

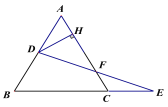
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在平面直角坐标系中，点、分别在轴和轴上，轴，.点从点出发，以1cm/s的速度沿边匀速运动，点从点出发，沿线段匀速运动.点与点同时出发，其中一点到达终点，另一点也随之停止运动.设点运动的时间为(s)，的面积为(cm2)，己知与之间的函数关系如图②中的曲线段、线段与曲线段.

    （1）点的运动速度为 cm/s，点的坐标为 ;

    （2）求曲线段的函数解析式;

    （3）当为何值时，的面积是四边形的面积的

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知Rt△ABC中，∠ACB＝90°，CA＝CB＝4，另有一块等腰直角三角板的直角顶点放在C处，CP＝CQ＝2，将三角板CPQ绕点C旋转（保持点P在△ABC内部），连接AP、BP、BQ．

    （1）如图1求证：AP＝BQ；

    （2）如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时，求AP的长；

    （3）设射线AP与射线BQ相交于点E，连接EC，写出旋转过程中EP、EQ、EC之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等边三角形ABC，点D是边AC上任意一点，延长BC至E，使CE＝AD．

    （1）如图1，点D是AC中点，求证：DB＝DE；

    （2）如图2，点D不是AC中点，求证：DB＝DE；

    （3）如图3，点D不是AC中点，点F是BD的中点，连接AE，AF，求证：AE＝2AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点，在抛物线上，且在该抛物线对称轴的同侧（点在点的左侧），过点、分别作轴的垂线，分别交轴于点、，交直线于点、．设为四边形的面积．则下列关系正确的是( )

    A. S=y2+y1 B. S=y2+2y1 C. S=y2-y1 D. S=y2-2y1

    查看答案和解析>>

    同步练习册答案