
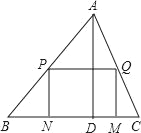
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
(1)若这个矩形是正方形,那么边长是多少?
(2)当PQ的值为多少时,这个矩形面积最大,最大面积是多少?
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣x2+4x﹣3,把抛物线C1先向右平移3个单位长度,再向上平移3个单位长度,得到抛物线C2, 将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M.若直线y=kx+ ![]() (k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
(k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
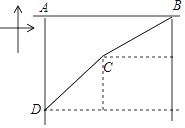
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
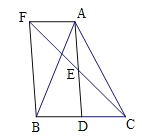
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:△AEF≌△DEC;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为 亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的![]() ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红从剩下的3个小球中随机取出一个小球,记下数字为 y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)以坐标原点为圆心,4为半径作圆,求出点(x,y)在圆内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)sin2 1°+sin2 2°+sin2 3°+…+sin2 87°+sin2 88°+sin2 89°
(2)sin2 66°-tan54°tan36°+sin2 24°+sin230°+cos230°+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com