
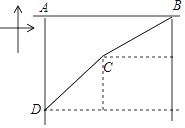
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
科目:初中数学 来源: 题型:
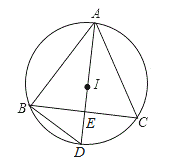
【题目】如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD.
(1)线段BD与ID相等吗?证明你的结论.
(2)证明:ID2=DEAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程x4﹣6x2+5=0,这是一个一元四次方程,根据该方程的特点,通常解法是:设x2=y,则原方程变形为关于y的方程y2﹣6y+5=0①,解得y1=1,y2=5,从而x2=1,x=±1或x2=5,x=±![]() ,所以原方程有四个根x1=
,所以原方程有四个根x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=1,x4=﹣1.
,x3=1,x4=﹣1.
(1)填空:由原方程得到方程①的过程中,利用 法达到降次的目的,体现了 的数学思想.
(2)解方程(x+1)(x+2)(x+3)(x+4)=120.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为圆心的圆过点A(0,3![]() ),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
A. 5 B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=![]() ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
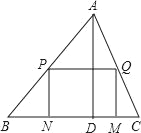
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
(1)若这个矩形是正方形,那么边长是多少?
(2)当PQ的值为多少时,这个矩形面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
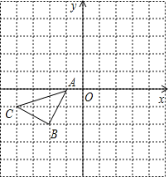
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
(1)分别写出点A的坐标 ,点B的坐标 .
(2)作出△ABC关于原点成中心对称的△A1B1C1;
(3)已知点M的坐标为(1,﹣4),请你在x轴上找一点P,使得PM+PB的值最小,并直接写出点P的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
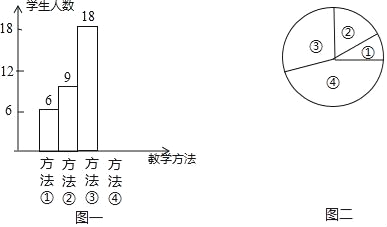
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com