
����Ŀ���ⷽ��x4��6x2+5��0������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬ͨ���ⷨ�ǣ���x2��y����ԭ���̱���Ϊ����y�ķ���y2��6y+5��0�٣����y1��1��y2��5���Ӷ�x2��1��x����1��x2��5��x����![]() ������ԭ�������ĸ���x1��
������ԭ�������ĸ���x1��![]() ��x2����
��x2����![]() ��x3��1��x4����1��
��x3��1��x4����1��
��1����գ���ԭ���̵õ����̢ٵĹ����У������� �����ﵽ���ε�Ŀ�ģ��������� ������ѧ˼�룮
��2���ⷽ�̣�x+1����x+2����x+3����x+4����120��
���𰸡���1����Ԫ��ת��;��2��x1��1��x2����6��
��������
��1����x2=y��ԭ������x4=y2��-6x2=-6y����x2ȫ����Ԫ��y�����û�Ԫ���ﵽ���ε�Ŀ�ģ�������ת������ѧ˼�룬
��2����x+1����x+4��=x2+5x+4����x+2����x+3��=x2+5x+6����x2+5x=y����ԭ���̱���Ϊ����y�ķ��̣�y+4����y+6��=120�����y��ֵ������x��ֵ���ɣ�
��1����x2��y��
��ԭ������x4��y2����6x2����6y��
��x2ȫ����Ԫ��y��
���û�Ԫ���ﵽ���ε�Ŀ�ģ�������ת������ѧ˼�룬
�ʴ�Ϊ����Ԫ��ת����
��2����x+1����x+4����x2+5x+4����x+2����x+3����x2+5x+6��
��x2+5x��y��
��ԭ���̱���Ϊ����y�ķ��̣�y+4����y+6����120��
��ã�y��6��16��
��x2+5x��6��x2+5x����16��
��һԪ���η���x2+5x��6�ã�x1��1��x2����6��
����x2+5x����16��ʵ������
��ԭ���̵Ľ�Ϊ��x1��1��x2����6��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4������ֱ��������![]() �IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊ
�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊ![]() ������һ�������ȷֳ�4�ݵ�ת�̣�����ֱ��������
������һ�������ȷֳ�4�ݵ�ת�̣�����ֱ��������![]() ��ת��ת����ָ����ָ�����ּ�Ϊ
��ת��ת����ָ����ָ�����ּ�Ϊ![]() ����ָ��ָ�ڷָ�����������תһ�Σ������
����ָ��ָ�ڷָ�����������תһ�Σ������![]() ����������
����������![]() ��
��![]() ����Χ�ɵ������ڣ������߽磩�ĸ�����__________��
����Χ�ɵ������ڣ������߽磩�ĸ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��a��0����ͼ����ͼ��ʾ�������н�������ȷ����
��a��0����ͼ����ͼ��ʾ�������н�������ȷ����
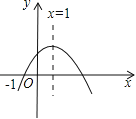
A. a��0 B. ����1��x��3ʱ��y��0
C. c��0 D. ��x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ֱ�������ľ������Ӱ�ӵ����Σ�

��1���ĸ�ͼ��ӳ��̫�����µ����Σ��ĸ�ͼ��ӳ��·���µ����Σ�
��2����̫�����£���֪С����������1.8�ף�Ӱ����1.2�ף���˵�Ӱ����4�ף�����˵ĸߣ�
��3������ͼ�зֱ���ʾ������ľ����Ӱ�����߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ת���ľ���ת��![]() �������ֳ���3�ȷݣ�����ÿ���ھ��������֣���ͼ��ʾ���������£�
�������ֳ���3�ȷݣ�����ÿ���ھ��������֣���ͼ��ʾ���������£�
���ֱ�ת��ת��![]() ��
��
������ת��ֹͣ������ָ����ָ���ڵ�������ˣ���ָ��ֹͣ�ڵȷ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ��Ϊֹ����

��1�����б�������״ͼ�ֱ��������֮��Ϊ3�ı���������֮��Ϊ5�ı����ĸ��ʣ�
��2��С����С������������ת������Ϸ�����ǹ涨������֮��Ϊ3�ı���ʱ��С����2�֣�����֮��Ϊ5�ı���ʱ��С����3�֣������Ϸ��˫����ƽ����˵�����ɣ���Ϊ����ƽ�ģ����ĵ÷ֹ涨��ʹ��Ϸ��˫����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y=��10x+500�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�������2000Ԫ����ôС��ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
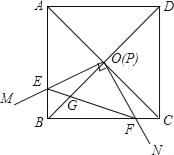
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��ֱ�ǡ�MPN�Ķ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ����_____.
��1��EF=![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3������ת�����У�����BEF���COF�����֮�����ʱ��AE=
OE����2��S�ı���OEBF��S������ABCD=1��4����3������ת�����У�����BEF���COF�����֮�����ʱ��AE=![]() ����4��OGBD=AE2+CF2.
����4��OGBD=AE2+CF2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
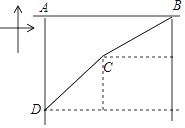
����Ŀ����ͼ����һ�ξ�����ϰ�У�������һ����������Ĺ�·�ϵ�A�������Ϸ����ˣ���·�Ͼ�A��45ǧ�ĺ췽��B������ƫ��67�㷽��ǰ��ʵʩ���أ��췽��ʻ26ǧ����C������ǰ����ͨ�У��췽�������������ٳ���ƫ��37�㷽��ǰ�����պ���D���ɹ����������������ص�D������·�ľ���AD�����ο����ݣ�sin67���![]() ��cos67���
��cos67���![]() ��tan67���
��tan67���![]() ��sin37���
��sin37���![]() ��cos37���
��cos37���![]() ��tan37���
��tan37���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���C=90�������н��ۣ���1��sinA��1����2����A��60������cosA��![]() ����3����A��45������sinA��cosA��������ȷ���У�������
����3����A��45������sinA��cosA��������ȷ���У�������
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com