
【题目】在Rt△ABC中,∠C=90°,下列结论:(1)sinA<1;(2)若A>60°,则cosA>![]() ;(3)若A>45°,则sinA>cosA.其中正确的有( )
;(3)若A>45°,则sinA>cosA.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
科目:初中数学 来源: 题型:
【题目】解方程x4﹣6x2+5=0,这是一个一元四次方程,根据该方程的特点,通常解法是:设x2=y,则原方程变形为关于y的方程y2﹣6y+5=0①,解得y1=1,y2=5,从而x2=1,x=±1或x2=5,x=±![]() ,所以原方程有四个根x1=
,所以原方程有四个根x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=1,x4=﹣1.
,x3=1,x4=﹣1.
(1)填空:由原方程得到方程①的过程中,利用 法达到降次的目的,体现了 的数学思想.
(2)解方程(x+1)(x+2)(x+3)(x+4)=120.
查看答案和解析>>
科目:初中数学 来源: 题型:
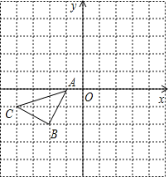
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
(1)分别写出点A的坐标 ,点B的坐标 .
(2)作出△ABC关于原点成中心对称的△A1B1C1;
(3)已知点M的坐标为(1,﹣4),请你在x轴上找一点P,使得PM+PB的值最小,并直接写出点P的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
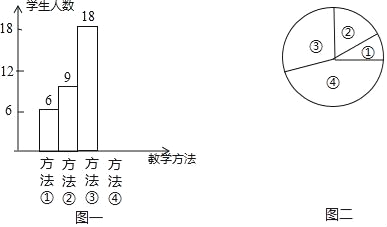
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=-![]() x2+bx+c(a≠0)的图象与x轴交于点A(-3,0)、B(1,0),顶点为C.
x2+bx+c(a≠0)的图象与x轴交于点A(-3,0)、B(1,0),顶点为C.
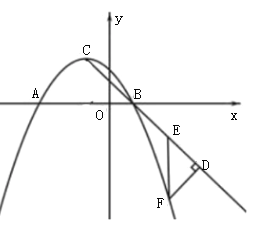
(1)求该二次函数的解析式和顶点C的坐标;
(2)如图,过B、C两点作直线,并将线段BC沿该直线向下平移,点B、C分别平移到点D、E处.若点F在这个二次函数的图象上,且△DEF是以EF为斜边的等腰直角三角形,求点F的坐标;
(3)试确定实数p,q的值,使得当p≤x≤q时,P≤y≤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
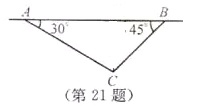
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
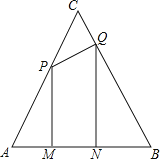
【题目】如图,等边三角形ABC的边长为8cm,动点P从点A出发以![]() 秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以
秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以![]() 秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、
秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、![]() 设P、Q两点运动时间为t秒
设P、Q两点运动时间为t秒![]() ,四边形MNQP的面积为
,四边形MNQP的面积为![]() .
.
![]() 为何值时,
为何值时,![]() 为等边三角形?
为等边三角形?
![]() 是否存在某一时刻t,使四边形MNQP的面积S等于
是否存在某一时刻t,使四边形MNQP的面积S等于![]() 的面积的
的面积的![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
![]() 连接PN、QM交于点D,是否存在某一时刻t,使
连接PN、QM交于点D,是否存在某一时刻t,使![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com