
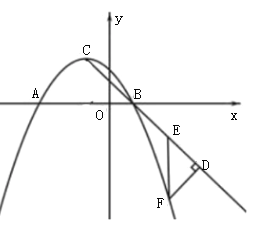
ЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§y=-![]() x2+bx+c(aЁй0)ЕФЭМЯѓгыxжсНЛгкЕуA(-3ЃЌ0)ЁЂBЃЈ1ЃЌ0ЃЉЃЌЖЅЕуЮЊC.
x2+bx+c(aЁй0)ЕФЭМЯѓгыxжсНЛгкЕуA(-3ЃЌ0)ЁЂBЃЈ1ЃЌ0ЃЉЃЌЖЅЕуЮЊC.
(1)ЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНКЭЖЅЕуCЕФзјБъЃЛ
(2)ШчЭМЃЌЙ§BЁЂCСНЕузїжБЯпЃЌВЂНЋЯпЖЮBCбиИУжБЯпЯђЯТЦНвЦЃЌЕуBЁЂCЗжБ№ЦНвЦЕНЕуDЁЂEДІЃЎШєЕуFдкетИіЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЧвЁїDEFЪЧвдEFЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌЧѓЕуFЕФзјБъЃЛ
(3)ЪдШЗЖЈЪЕЪ§pЃЌqЕФжЕЃЌЪЙЕУЕБpЁмxЁмqЪБЃЌPЁмyЁм![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖЅЕуCЃЈ-1ЃЌ2ЃЉЃЛЃЈ2ЃЉFЃЈ3ЃЌ-6ЃЉЃЛЃЈ3ЃЉp=-2-![]() ЃЌq=-2Лђp=0,q=1
ЃЌq=-2Лђp=0,q=1
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУНтЮіЪНЃЌАбНтЮіЪНЛЏГЩЖЅЕуЪНМДПЩЧѓЕУЖЅЕузјБъЃЛ
ЃЈ2ЃЉЙ§ЕуCзї![]() жсгкЕуH,ИљОнЙДЙЩЖЈРэЧѓГі
жсгкЕуH,ИљОнЙДЙЩЖЈРэЧѓГі![]() ИљОнЦНвЦвдМАЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕН
ИљОнЦНвЦвдМАЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕН![]() ИљОнЙДЙЩЖЈРэЧѓГі
ИљОнЙДЙЩЖЈРэЧѓГі![]() жЄУї
жЄУї![]() ЃЌЩшЕуF
ЃЌЩшЕуF![]() Цфжа
Цфжа![]() Еу
Еу![]() СаГіЗНГЬМДПЩЧѓГі
СаГіЗНГЬМДПЩЧѓГі![]() ЕФжЕЃЌМДПЩЧѓНт.
ЕФжЕЃЌМДПЩЧѓНт.
ЃЈ3ЃЉЗжЂйЕБ![]() ЪБЃЌ ЂкЕБ
ЪБЃЌ ЂкЕБ![]() ЪБЃЌЂлЕБ
ЪБЃЌЂлЕБ![]() ЪБШ§жжЧщПіНјааЬжТл.
ЪБШ§жжЧщПіНјааЬжТл.
(1)ЁпХзЮяЯп![]() ОЙ§ЕуA(3,0)КЭB(1,0)ЃЌ
ОЙ§ЕуA(3,0)КЭB(1,0)ЃЌ
Ёр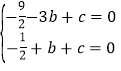 НтЕУ
НтЕУ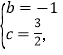
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]()
Ёп![]()
ЁрЖЅЕуCЕФзјБъЮЊ(1,2)ЃЛ
(2)ШчЭМЃЌ
Й§ЕуCзї![]() жсгкЕуH,
жсгкЕуH,
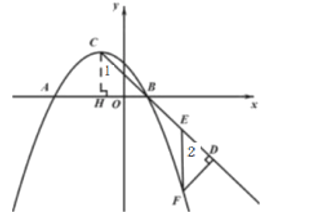
![]()
![]()
![]()
![]()
![]()
дкЕШбќжБНЧ![]() жаЃЌ
жаЃЌ
![]()
![]()
![]()
![]() ЃЌ
ЃЌ![]()
![]() ПЩЕУжБЯпBCЕФНтЮіЪНЮЊЃК
ПЩЕУжБЯпBCЕФНтЮіЪНЮЊЃК![]()
гЩЬтвтЃЌЩшЕуF![]() Цфжа
Цфжа![]()
дђЕу![]()
![]()
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
![]()
ЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
НтЕУЃК![]()
![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ2ЃЌ
газюДѓжЕ2ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЗжШ§жжЧщПіНјааЬжТл:
ЂйЕБ![]() ЪБЃЌгЩдіМѕадЕУЃКЕБ
ЪБЃЌгЩдіМѕадЕУЃКЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]()
![]() ЪБЃЌ
ЪБЃЌ![]() ДњШы
ДњШы![]()
НтЕУЃК![]() ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЃЈВЛКЯЬтвтЩсШЅЃЉ
![]()
ЂкЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]() ВЛКЯЬтвт.
ВЛКЯЬтвт.
ЂлЕБ![]() ЪБЃЌгЩдіМѕадЕУЃКЕБ
ЪБЃЌгЩдіМѕадЕУЃКЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]()
![]() ЪБЃЌ
ЪБЃЌ![]() ДњШы
ДњШы![]()
![]()
НтЕУЃК![]() ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЃЈВЛКЯЬтвтЩсШЅЃЉ
![]()
злЩЯЫљЪіЃЌТњзуЬѕМўЕФpЃЌqЕФжЕЮЊ![]() Лђ
Лђ![]()


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаСНИіПЩвдздгЩзЊЖЏЕФОљдШзЊХЬ![]() ЃЌЖМБЛЗжГЩСЫ3ЕШЗнЃЌВЂдкУПЗнФкОљБъгаЪ§зжЃЌШчЭМЫљЪОЃЎЙцдђШчЯТЃК
ЃЌЖМБЛЗжГЩСЫ3ЕШЗнЃЌВЂдкУПЗнФкОљБъгаЪ§зжЃЌШчЭМЫљЪОЃЎЙцдђШчЯТЃК
ЂйЗжБ№зЊЖЏзЊХЬ![]() ЃЛ
ЃЛ
ЂкСНИізЊХЬЭЃжЙКѓЃЌНЋСНИіжИеыЫљжИЗнФкЕФЪ§зжЯрГЫЃЈШєжИеыЭЃжЙдкЕШЗнЯпЩЯЃЌФЧУДжизЊвЛДЮЃЌжБЕНжИеыжИЯђФГвЛЗнЮЊжЙЃЉЃЎ

ЁО1ЁПгУСаБэЗЈЛђЪїзДЭМЗжБ№ЧѓГіЪ§зжжЎЛ§ЮЊ3ЕФБЖЪ§КЭЪ§зжжЎЛ§ЮЊ5ЕФБЖЪ§ЕФИХТЪЃЛ
ЁО2ЁПаЁУїКЭаЁССЯыгУетСНИізЊХЬзігЮЯЗЃЌЫћУЧЙцЖЈЃКЪ§зжжЎЛ§ЮЊ3ЕФБЖЪ§ЪБЃЌаЁУїЕУ2ЗжЃЛЪ§зжжЎЛ§ЮЊ5ЕФБЖЪ§ЪБЃЌаЁССЕУ3ЗжЃЎетИігЮЯЗЖдЫЋЗНЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЛШЯЮЊВЛЙЋЦНЕФЃЌЪдаоИФЕУЗжЙцЖЈЃЌЪЙгЮЯЗЖдЫЋЗНЙЋЦНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љx+m=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЗНГЬЕФСНИіЪЕЪ§ИљЮЊx1ЁЂx2ЃЌЧвx1+x2+x1x2=m2Љ1ЃЌЧѓЪЕЪ§mЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
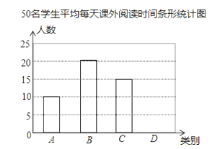
ЁОЬтФПЁППЮЭтдФЖСЪЧЬсИпбЇЩњЫибјЕФживЊЭООЖЃЎФГаЃЮЊСЫНтбЇЩњПЮЭтдФЖСЧщПіЃЌЫцЛњГщВщСЫ50УћбЇЩњЃЌЭГМЦЫћУЧЦНОљУПЬьПЮЭтдФЖСЪБМфtЃЈаЁЪБЃЉЃЎИљОнtЕФГЄЖЬЗжЮЊAЃЌBЃЌCЃЌDЫФРрЃЌЯТУцЪЧИљОнЫљГщВщЕФШЫЪ§ЛцжЦЕФСНЗљВЛЭъећЕФЭГМЦЭМБэЃЎЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТУцЕФЮЪЬтЃК
50УћбЇЩњЦНОљУПЬьПЮЭтдФЖСЪБМфЭГМЦБэ
РрБ№ | ЪБМфtЃЈаЁЪБЃЉ | ШЫЪ§ |
A | tЃМ0.5 | 10 |
B | 0.5ЁмtЃМ1 | 20 |
C | 1ЁмtЃМ1.5 | 15 |
D | tЁн1.5 | a |
ЃЈ1ЃЉБОДЮЕїВщЕФбљБОШнСПЮЊЖрЩйЃП
ЃЈ2ЃЉЧѓБэИёжаЕФaЕФжЕЃЌВЂдкЭМжаВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃЯжга1200УћбЇЩњЃЌЧыФуЙРМЦИУаЃЙВгаЖрЩйУћбЇЩњПЮЭтдФЖСЪБМфВЛЩйгк1аЁЪБЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
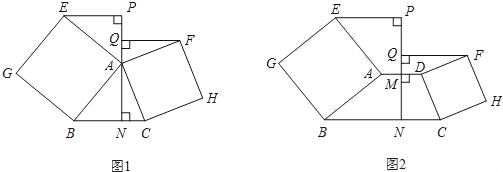
ЁОЬтФПЁПЃЈ1ЃЉвбжЊЃКШчЭМ1ЃЌЁїABCжаЃЌЗжБ№вдABЁЂACЮЊвЛБпЯђЁїABCЭтзїе§ЗНаЮABGEКЭACHFЃЌжБЯпANЁЭBCгкNЃЌШєEPЁЭANгкPЃЌFQЁЭANгкQЃЎХаЖЯЯпЖЮEPЁЂFQЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЬнаЮABCDжаЃЌADЁЮBCЃЌЗжБ№вдСНбќABЁЂCDЮЊвЛБпЯђЬнаЮABCDЭтзїе§ЗНаЮABGEКЭDCHFЃЌЯпЖЮADЕФДЙжБЦНЗжЯпНЛЯпЖЮADгкЕуMЃЌНЛBCгкЕуNЃЌШєEPЁЭMNгкPЃЌFQЁЭMNгкQЃЎЃЈ1ЃЉжаНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЯТСаНсТлЃКЃЈ1ЃЉsinAЃМ1ЃЛЃЈ2ЃЉШєAЃО60ЁуЃЌдђcosAЃО![]() ЃЛЃЈ3ЃЉШєAЃО45ЁуЃЌдђsinAЃОcosAЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЛЃЈ3ЃЉШєAЃО45ЁуЃЌдђsinAЃОcosAЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
A. 0Иі B. 1Иі C. 2Иі D. 3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=Љx2Љ2x+3гУХфЗНЗЈЛЏГЩy=aЃЈxЉhЃЉ2+kЕФаЮЪНЪЧ________ЃЌХзЮяЯпгыxжсЕФНЛЕузјБъЪЧ________ЃЌХзЮяЯпгыyжсЕФНЛЕузјБъЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
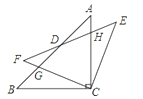
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌBC=ACЃЌЁЯACB=90ЁуЃЌНЋЁїABCШЦзХЕуCЫГЪБеыа§зЊІСЁуЃЈ0ЁмІСЁм90ЁуЃЉЃЌЕУЕНЁїEFCЃЌEFгыABЁЂACЯрНЛгкЕуDЁЂHЃЌFCгыABЯрНЛгкЕуGЁЂACЯрНЛгкЕуDЁЂHЃЌFCгыABЯрНЯгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїGBCЁеЁїHECЃЛ
ЃЈ2ЃЉдка§зЊЙ§ГЬжаЃЌЫФБпаЮBCEDПЩвдЪЧФГжжЬиЪтЕФЦНааЫФБпаЮЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкПЮЬУЩЯЃЌРЯЪІНЋГ§беЩЋЭтЖМЯрЭЌЕФ1ИіКкЧђКЭШєИЩИіАзЧђЗХШывЛИіВЛЭИУїЕФПкДќВЂНСдШЃЌШУШЋАрЭЌбЇвРДЮНјааУўЧђЪдбщЃЌУПДЮЫцЛњУўГівЛИіЧђЃЌМЧЯТбеЩЋдйЗХЛиНСдШЃЌЯТБэЪЧЪдбщЕУЕНЕФвЛзщЪ§ОнЃЎ
УўЧђЕФДЮЪ§n | 100 | 150 | 200 | 500 | 800 |
УўЕНКкЧђЕФДЮЪ§m | 26 | 37 | 49 | 124 | 200 |
УўЕНКкЧђЕФЦЕТЪ |
|
|
|
| a |
![]() БэжаaЕФжЕЕШгк______ЃЛ
БэжаaЕФжЕЕШгк______ЃЛ
![]() ЙРЫуПкДќжаАзЧђЕФИіЪ§ЃЛ
ЙРЫуПкДќжаАзЧђЕФИіЪ§ЃЛ
![]() гУЛЪїзДЭМЛђСаБэЕФЗНЗЈМЦЫуСЌајСНУћЭЌбЇЖМУўГіАзЧђЕФИХТЪЃЎ
гУЛЪїзДЭМЛђСаБэЕФЗНЗЈМЦЫуСЌајСНУћЭЌбЇЖМУўГіАзЧђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com