
【题目】如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
(1)求证:△GBC≌△HEC;
(2)在旋转过程中,四边形BCED可以是某种特殊的平行四边形?并说明理由.
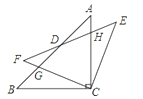
【答案】(1)详见解析;(2)当α=45°时,四边形BCED为菱形,理由详见解析.
【解析】
(1)先判断△ABC为等腰直角三角形得到∠A=∠B=45°,再根据旋转的性质得∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,于是可根据“ASA”判断△GBC≌△HEC;
(2)当α=45°时,如图,根据旋转的性质得∠BCF=∠ACE=45°,则可计算出∠BCE=∠BCA+∠ACE=135°,所以∠B+∠BCE=180°,∠E+∠BCE=180°,所以BD∥CE,BC∥DE,于是可判断四边形BCED为平行四边形,加上CB=CE,则可判断四边形BCED为菱形.
(1)证明:∵BC=AC,∠ACB=90°,
∴△ABC为等腰直角三角形,
∴∠A=∠B=45°,
∵△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,
∴∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,
在△GBC和△HEC中
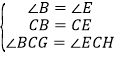 ,
,
∴△GBC≌△HEC;
(2)解:当α=45°时,四边形BCED为菱形.理由如下:
如图,∵∠BCF=∠ACE=45°,
∴∠BCE=∠BCA+∠ACE=90°+45°=135°,
而∠E=∠B=45°,
∴∠B+∠BCE=180°,∠E+∠BCE=180°,
∴BD∥CE,BC∥DE,
∴四边形BCED为平行四边形,
∵CB=CE,
∴四边形BCED为菱形.


科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=![]() ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=-![]() x2+bx+c(a≠0)的图象与x轴交于点A(-3,0)、B(1,0),顶点为C.
x2+bx+c(a≠0)的图象与x轴交于点A(-3,0)、B(1,0),顶点为C.
(1)求该二次函数的解析式和顶点C的坐标;
(2)如图,过B、C两点作直线,并将线段BC沿该直线向下平移,点B、C分别平移到点D、E处.若点F在这个二次函数的图象上,且△DEF是以EF为斜边的等腰直角三角形,求点F的坐标;
(3)试确定实数p,q的值,使得当p≤x≤q时,P≤y≤![]() .
.
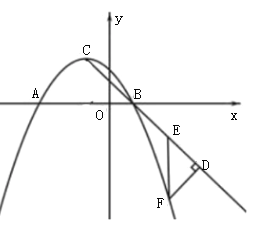
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
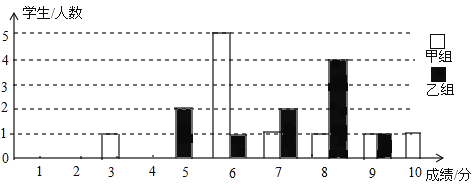
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形,![]() 与
与![]() 是关于点
是关于点![]() 为位似中心的位似图形,它们的顶点都在小正方形的顶点上。
为位似中心的位似图形,它们的顶点都在小正方形的顶点上。
(1)在图中画出位似中心点![]() ,
,![]() 与
与![]() 的相似比是_________;
的相似比是_________;
(2)以点![]() 为位似中心,再画一个
为位似中心,再画一个![]() ,使它与
,使它与![]() 的相似比等于
的相似比等于![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com