
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
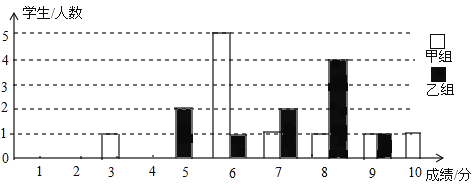
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
【答案】解:(1)填表如下:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 6 | 3.41 | 90% | 20% |
乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)甲。
(3)乙组的平均分,中位数高于甲组,方差小于甲组,故乙组成绩好于甲组。
故答案为:(1)6;7.1;(2)甲
【解析】
(1)将甲组成绩按照从小到大的顺序排列,找出第5、6个成绩,求出平均数即为甲组的中位数;找出乙组成绩,求出乙组的平均分,填表即可:
∵甲组的成绩为:3,6,6,6,6,6,7,8,9,10,∴甲组中位数为6分。
∵乙组成绩为5,5,6,7,7,8,8,8,8,9,平均分为![]() (分)。
(分)。
(2)根据两组的中位数,观察表格,成绩为7分处于中游略偏上,应为甲组的学生。
(3)乙组的平均分高于甲组,中位数高于甲组,方差小于甲组,所以乙组成绩好于甲组。
解:(1)填表如下:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 6 | 3.41 | 90% | 20% |
乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)甲。
(3)乙组的平均分,中位数高于甲组,方差小于甲组,故乙组成绩好于甲组。
故答案为:(1)6;7.1;(2)甲


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
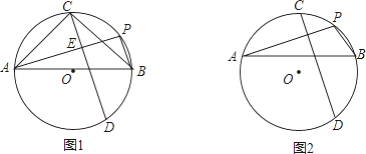
【题目】(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为![]() 的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧![]() 的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
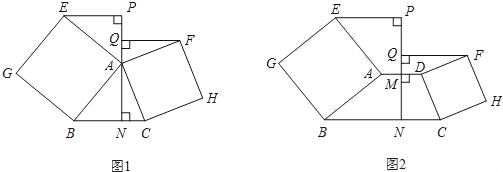
【题目】(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN于P,FQ⊥AN于Q.判断线段EP、FQ的数量关系,并证明;
(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P,FQ⊥MN于Q.(1)中结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2﹣2x+3用配方法化成y=a(x﹣h)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①对角线互相垂直且相等的平行四边形是正方形;
②平行四边形、矩形、等边三角形、正方形既是中心对称图形,也是轴对称图形;
③旋转和平移都不改变图形的形状和大小;
④底角是45°的等腰梯形,高是h,则腰长是![]() h;
h;
⑤一组对边平行,另一组对边相等的四边形是平行四边形.
以上正确的命题是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
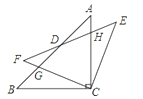
【题目】如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
(1)求证:△GBC≌△HEC;
(2)在旋转过程中,四边形BCED可以是某种特殊的平行四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段BE为何值时,线段AM最短,最短是多少?
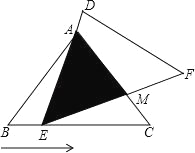
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张卡片(背面完全相同),分别写有数字1、2、﹣1、﹣2,把它们背面朝上洗匀后,甲同学抽取一张记下这个数字后放回洗匀,乙同学再从中抽出一张,记下这个数字,用字母b、c分别表示甲、乙两同学抽出的数字.
(1)用列表法求关于x的方程x2+bx+c=0有实数解的概率;
(2)求(1)中方程有两个相等实数解的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com