
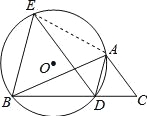
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)由圆周角定理,可得∠BAD=∠E,又由BE∥AD,易证得∠BAD=∠ADE,然后由AD是△ABC的角平分线,证得∠CAD=∠ADE,继而证得结论;
(2)首先连接AE,易得∠CAD=∠ABE,∠ADC=∠AEB,则可证得△ADC∽△BEA,然后由相似三角形的对应边成比例,证得结论.
试题解析:(1)∵BE∥AD,
∴∠E=∠ADE,
∵∠BAD=∠E,
∴∠BAD=∠ADE,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠CAD=∠ADE,
∴ED∥AC;
(2)连接AE,
∵∠CAD=∠ADE,∠ADE=∠ABE,
∴∠CAD=∠ABE,
∵∠ADC+∠ADB=180°,∠ADB+∠AEB=180°,
∴∠ADC=∠AEB,
∴△ADC∽△BEA,
∴AC:AB=CD:AE,
∴ABCD=AEAC.


科目:初中数学 来源: 题型:
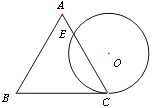
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是:
A. ![]() B.
B. ![]() C. 2 D. 3
C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
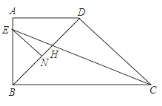
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(![]() +1)EH;③
+1)EH;③![]() =
=![]() . 其中正确的是( )
. 其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为圆心的圆过点A(0,3![]() ),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
A. 5 B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
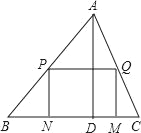
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
(1)若这个矩形是正方形,那么边长是多少?
(2)当PQ的值为多少时,这个矩形面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了![]() 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):
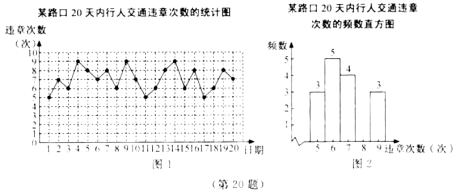
请根据所给信息,解答下列问题:
(1)第![]() 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这![]() 天中,行人交通违章
天中,行人交通违章![]() 次的有多少天?
次的有多少天?
(2)请把图2中的频数直方图补充完整;(温馨提示:请画在答题卷相对应的图上)
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了![]() 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
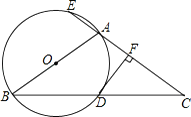
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com