
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
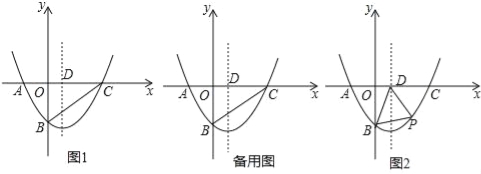
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)(8﹣2
x﹣4;(2)(8﹣2![]() ,﹣
,﹣![]() )、(0,﹣4)、(
)、(0,﹣4)、(![]() ,﹣
,﹣![]() );(3)(
);(3)(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)∵二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,∴![]() ,解得
,解得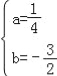 ,∴该二次函数的解析式为y=
,∴该二次函数的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)由二次函数y=![]() x2﹣
x2﹣![]() x﹣4可知对称轴x=3,∴D(3,0),∵C(8,0),∴CD=5,由二次函数y=
x﹣4可知对称轴x=3,∴D(3,0),∵C(8,0),∴CD=5,由二次函数y=![]() x2﹣
x2﹣![]() x﹣4可知B(0,﹣4),设直线BC的解析式为y=kx+b,∴
x﹣4可知B(0,﹣4),设直线BC的解析式为y=kx+b,∴![]() ,解得
,解得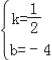 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣4,设E(m,
x﹣4,设E(m,![]() m﹣4),当DC=CE时,EC2=(m﹣8)2+(
m﹣4),当DC=CE时,EC2=(m﹣8)2+(![]() m﹣4)2=CD2,即(m﹣8)2+(
m﹣4)2=CD2,即(m﹣8)2+(![]() m﹣4)2=52,解得m1=8﹣2
m﹣4)2=52,解得m1=8﹣2![]() ,m2=8+2
,m2=8+2![]() (舍去),∴E(8﹣2
(舍去),∴E(8﹣2![]() ,﹣
,﹣![]() );当DC=DE时,ED2=(m﹣3)2+(
);当DC=DE时,ED2=(m﹣3)2+(![]() m﹣4)2=CD2,即(m﹣3)2+(
m﹣4)2=CD2,即(m﹣3)2+(![]() m﹣4)2=52,解得m3=0,m4=8(舍去),∴E(0,﹣4);当EC=DE时,(m﹣8)2+(
m﹣4)2=52,解得m3=0,m4=8(舍去),∴E(0,﹣4);当EC=DE时,(m﹣8)2+(![]() m﹣4)2=(m﹣3)2+(
m﹣4)2=(m﹣3)2+(![]() m﹣4)2解得m5=5.5,∴E(
m﹣4)2解得m5=5.5,∴E(![]() ,﹣
,﹣![]() ).综上,存在点E,使得△CDE为等腰三角形,所有符合条件的点E的坐标为(8﹣2
).综上,存在点E,使得△CDE为等腰三角形,所有符合条件的点E的坐标为(8﹣2![]() ,﹣
,﹣![]() )、(0,﹣4)、(
)、(0,﹣4)、(![]() ,﹣
,﹣![]() ).
).
(3)过点P作y轴的平行线交x轴于点F,∵P点的横坐标为m,∴P点的纵坐标为![]() m2﹣
m2﹣![]() m﹣4,∵△PBD的面积S=S梯形﹣S△BOD﹣S△PFD=
m﹣4,∵△PBD的面积S=S梯形﹣S△BOD﹣S△PFD=![]() m[4﹣(
m[4﹣(![]() m2﹣
m2﹣![]() m﹣4)]﹣
m﹣4)]﹣![]() (m﹣3)[﹣(
(m﹣3)[﹣(![]() m2﹣
m2﹣![]() m﹣4)]﹣
m﹣4)]﹣![]() ×3×4=﹣
×3×4=﹣![]() m2+
m2+![]() m=﹣
m=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,∴当m=
,∴当m=![]() 时,△PBD的最大面积为
时,△PBD的最大面积为![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
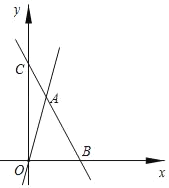
【题目】已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,得到一个边长为
,得到一个边长为![]() 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证![]() 的方案(详见方案1)
的方案(详见方案1)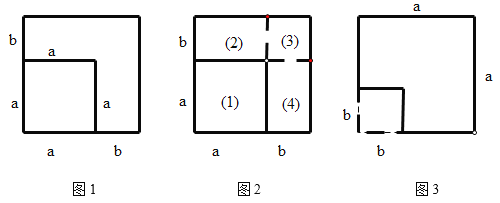
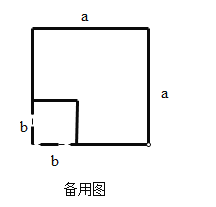
方案1.如图2,用两种不同的方式表示边长为![]() 的正方形的面积.
的正方形的面积.
方式1:![]()
方式2:![]()
因此,![]()
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证![]() ;
;
(2)如图3,在边长为![]() 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为![]() 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE,若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为( )
的值为( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至![]() 处,
处,![]() 与CE交于点F,若∠B=52°,∠DAE=20°,则
与CE交于点F,若∠B=52°,∠DAE=20°,则![]() 的度数为( )
的度数为( )
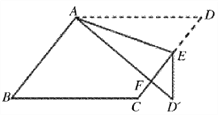
A. 40° B. 36° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城镇在对一项工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲队工程款2万元,付乙队工程款1.5万元.现有三种施工方案:(![]() )由甲队单独完成这项工程,恰好如期完工;(
)由甲队单独完成这项工程,恰好如期完工;(![]() )由乙队单独完成这项工程,比规定工期多6天;(
)由乙队单独完成这项工程,比规定工期多6天;(![]() )由甲乙两队
)由甲乙两队![]() 后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为
后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为![]() 天,依题意列出方程:
天,依题意列出方程:![]() .
.
(1)请将(![]() )中被墨水污染的部分补充出来:________;
)中被墨水污染的部分补充出来:________;
(2)你认为三种施工方案中,哪种方案既能如期完工,又节省工程款?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
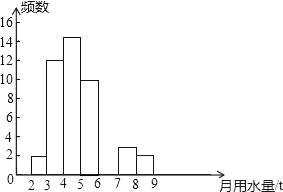
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com