
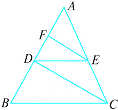
【题目】如图所示,已知DE∥BC,EF平分∠AED,EF⊥AB,CD⊥AB,求证:CD平分∠ACB .
【答案】证明过程见解析
【解析】
试题分析:根据垂直得到 EF∥CD,从而说明∠FED=∠CDE和∠AEF=∠DCE,根据DE∥BC得出∠CDE=∠DCB,从而得出∠DCB=∠FED,根据角平分线得出∠AEF=∠FED,从而得到∠DCE=∠DCB,即角平分线.
试题解析:∵ EF⊥AB,CD⊥AB (已知),
∴ EF∥CD (垂直于同一条直线的两直线平行).
∴∠FED=∠CDE(两直线平行,内错角相等),∠AEF=∠DCE(两直线平行,同位角相等).
∵ DE∥BC(已知),
∴∠CDE=∠DCB(两直线平行,内错角相等),
∴∠DCB=∠FED (等量代换).
∵ EF平分∠AED (已知),
∴∠AEF=∠FED(角平分线性质).
∴∠DCE=∠DCB(等量代换).
∴ CD平分∠ACB(角平分线性质).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】完成下面证明:
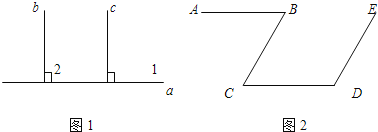
(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b
证明:∵a⊥c ( 已知 )
∴∠1= ( 垂直定义)
∵b∥c (已知 )
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知 )
∴∠B= ( )
∵∠B+∠D=180° (已知 )
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
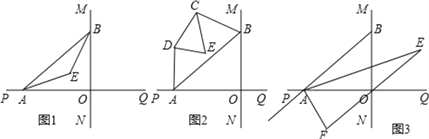
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=∠C,与△ABC全等的△DEF中有一个角是100°,那么在△ABC中与这100°角对应相等的角是( )
A. ∠A B. ∠B C. ∠C D. ∠B或∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①无限小数都是有理数;②不循环小数不是有理数;
③不是有理数的数都是无限小数;④0是有理数
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )

A.130° B.150° C.160° D.170°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“五一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:已知:用3600元购进甲种运动鞋的数量与用3000元购进乙种运动鞋的数量相同.

(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21600元,且不超过22440元,问该专卖店有多少种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com