
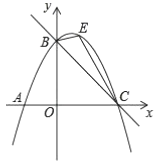
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
(2)如图,点![]() 是抛物线上的一动点(不与
是抛物线上的一动点(不与![]() ,
,![]() 两点重合),当
两点重合),当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上的一动点,当
是抛物线上的一动点,当![]() 为什么取值范围时,对应的点
为什么取值范围时,对应的点![]() 有且只有两个?
有且只有两个?
【答案】(1)![]() ;(2)
;(2)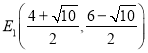 ,
,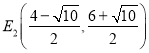 ,
,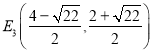 ,
,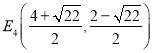 ;(3)当
;(3)当![]() 时,对应的点
时,对应的点![]() 有且只有两个.
有且只有两个.
【解析】
(1)根据待定系数法,即可求解;
(2)过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,设点
,设点![]() ,点
,点![]() ,根据
,根据![]() ,
,![]() ,列出方程,即可求解;
,列出方程,即可求解;
(3)当![]() 点在直线
点在直线![]() 的下方的抛物线上时,一定有两个对应的
的下方的抛物线上时,一定有两个对应的![]() 点满足
点满足![]() 面积为
面积为![]() ,当
,当![]() 点在直线
点在直线![]() 的上方的抛物线上时,无
的上方的抛物线上时,无![]() 点满足
点满足![]() 面积为
面积为![]() 才符合题意,故只需要求出当点
才符合题意,故只需要求出当点![]() 在直线
在直线![]() 的上方时,
的上方时,![]() 的最大值,即可得到结论 .
的最大值,即可得到结论 .
(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
可得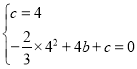 ,解得
,解得![]() ,
,
∴![]() ;
;
(2)如图,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,
,
设点![]() ,则点
,则点![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
将![]() ,
,![]() ,
,![]() ,
,![]() 代入抛物线解析式,可得:
代入抛物线解析式,可得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴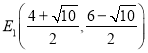 ,
,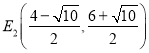 ,
,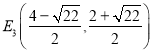 ,
,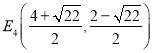 ;
;
(3)当点F在直线BC上方的抛物线上时,设点![]() ,
,
由(2)同理可得:![]() ,
,
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
∴当![]() >
>![]() 时,在直线BC的上方的抛物线上无法找到
时,在直线BC的上方的抛物线上无法找到![]() 点,
点,
综上所述:当![]() 时,对应的点
时,对应的点![]() 有且只有两个.
有且只有两个.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】中考让同学们感觉压力较大,初三某班班主任想通过课间播放音乐来帮助学生缓解压力,采用全面调查的方法调查了学生对音乐类型的兴趣爱好,结果全班学生选择集中在流行音乐、民族音乐、摇滚音乐和轻音乐四种音乐类型.根据调查的结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
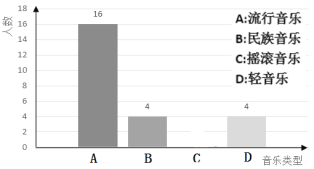
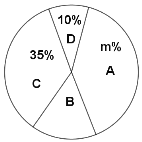
(1)求该班学生总人数,并把条形统计图补充完整;
(2)求扇形统计图中![]() 的值和表示流行音乐的扇形圆心角的度数;
的值和表示流行音乐的扇形圆心角的度数;
(3)班主任每天挑选出四种类型音乐各一首放在一个播放器内,每次随机播放两首不同音乐,请用画树状图或列表的方法求出某次恰好播放民族音乐和轻音乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
查看答案和解析>>
科目:初中数学 来源: 题型:
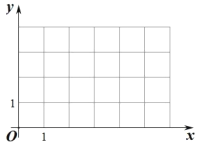
【题目】在平面直角坐标系![]() 中,我们把横、纵坐标都是整数的点叫做整点,已知点
中,我们把横、纵坐标都是整数的点叫做整点,已知点![]() ,点
,点![]() 是
是![]() 轴正半轴上的点,记
轴正半轴上的点,记![]() 内部(不包括边界)的整点个数为
内部(不包括边界)的整点个数为![]() ,当
,当![]() 时,点
时,点![]() 的横坐标
的横坐标![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+6与x轴交于点A,与y轴交于点B,在x轴上有一点E,在y轴上有一点F,满足OB=3BF=3AE,连接EF,交AB于点M,则M的坐标为_____.
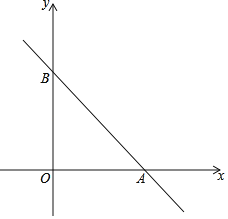
查看答案和解析>>
科目:初中数学 来源: 题型:
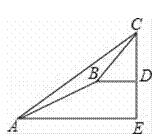
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
己知:如图1,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() 的平行直线,使它经过点
的平行直线,使它经过点![]() .
.

作法:如图2,
(1)过![]() 作直线
作直线![]() 与直线
与直线![]() 交于点
交于点![]() ;
;
(2)在直线![]() 取一点
取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与直线
长为半径画弧,与直线![]() 交于点
交于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() 以点
以点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;
;
(4)作直线![]() .
.
所以,直线![]() 就是所求作的平行线.
就是所求作的平行线.
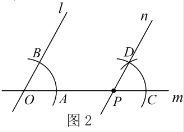
请回答:该作图的依据是______________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com