
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+6与x轴交于点A,与y轴交于点B,在x轴上有一点E,在y轴上有一点F,满足OB=3BF=3AE,连接EF,交AB于点M,则M的坐标为_____.
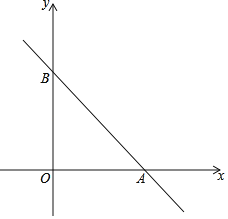
【答案】(2,4)或(4,2)
【解析】
先求出点A和点B的坐标,再根据OB=3BF=3AE,得出点E和点F的坐标,作出图形,求出直线EF和直线E'F'的解析式,然后分别与直线y=﹣x+6组成方程组,即可求得答案.
解:∵直线y=﹣x+6与x轴交于点A,与y轴交于点B,
∴A(6,0),B(0,6)
∵OB=3BF=3AE
∴E(4,0)或E'(8,0);F(0,8)或F'(0,4),如图所示,连接EF,E'F',分别交AB于点M和点M',
∴E'F∥AB∥EF'
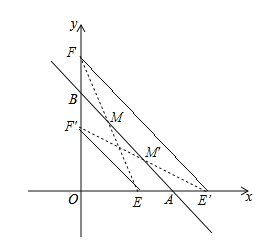
设直线EF的解析式为:y=mx+8,将E(4,0)代入得:
0=4m+8,
解得m=﹣2
∴y=﹣2x+8
由![]() 得:
得:![]()
∴M(2,4)
同理,设直线E'F'的解析式为:y=nx+4,将E'(8,0)代入得:
0=8n+4
解得:n=﹣![]()
∴y=﹣![]() x+4
x+4
由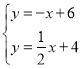
解得:![]()
∴M'(4,2)
故答案为:(2,4)或(4,2).


科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能状况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行统计,绘制成图(1)和图(2)两幅尚不完整的统计图.
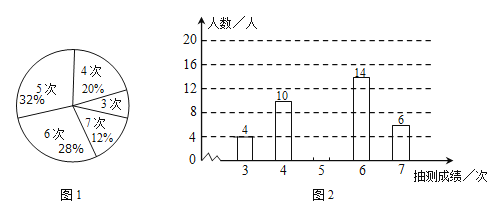
(1)本次抽取的男生有 人,抽取成绩的众数是 ;
(2)请你在图(2)补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,该校九年级男生共有900人,则估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)图象的一部分,与x轴的右交点在点(2,0)和(3,0)之间,对称轴是x=1,对于下列说法:①abc<0; ②2a+b=0; ③3a+c>0; ④当﹣1<x<2时,y>0; ⑤b2﹣4ac>0.其中正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
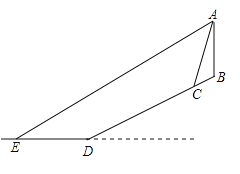
【题目】寒假期间,小明和好朋友一起前往三亚旅游.他们租住的宾馆![]() 坐落在坡度为
坐落在坡度为![]() 的斜坡上.宾馆
的斜坡上.宾馆![]() 高为129米.某天,小明在宾馆顶楼的海景房
高为129米.某天,小明在宾馆顶楼的海景房![]() 处向外看风景,发现宾馆前有一座雕像
处向外看风景,发现宾馆前有一座雕像![]() (雕像的高度忽略不计),已知雕像
(雕像的高度忽略不计),已知雕像![]() 距离海岸线
距离海岸线![]() 的距离
的距离![]() 为260米,与宾馆
为260米,与宾馆![]() 的水平距离为36米,远处海面上一艘即将靠岸的轮船
的水平距离为36米,远处海面上一艘即将靠岸的轮船![]() 的俯角为
的俯角为![]() .则轮船
.则轮船![]() 距离海岸线
距离海岸线![]() 的距离
的距离![]() 的长为( )
的长为( )
(参考数据:![]() ,
,![]() )
)
A.262米B.212米C.244米D.276米
查看答案和解析>>
科目:初中数学 来源: 题型:
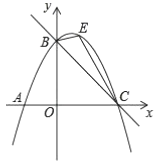
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
(2)如图,点![]() 是抛物线上的一动点(不与
是抛物线上的一动点(不与![]() ,
,![]() 两点重合),当
两点重合),当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上的一动点,当
是抛物线上的一动点,当![]() 为什么取值范围时,对应的点
为什么取值范围时,对应的点![]() 有且只有两个?
有且只有两个?
查看答案和解析>>
科目:初中数学 来源: 题型:
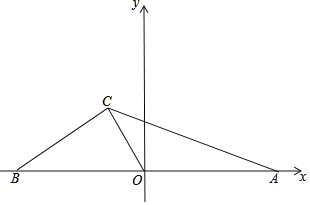
【题目】如图,在平面直角坐标系中,直线BC:y=![]() 交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,
交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,![]() )
)
(1)求线段CO的长;
(2)点D在OC的延长线上,连接AD,点E为AD的中点,连接CE,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式;
(3)在(2)的条件下,点F为射线BC上一点,连接DB、DF,且∠FDB=∠OBD,CE=![]() ,求此时S值及点F坐标.
,求此时S值及点F坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“五·四”文艺会演,5位评委给各班演出的节目打分.在5个评分中,去掉一个最高分,再去掉一个最低分,求出评分的平均数,作为该节目的实际得分,对于某节目的演出,评分如下8.9,9.1,9.3,9.4,9.2那么该节目实际得分是( )
A.9.4B.9.3C.9.2D.9.18
查看答案和解析>>
科目:初中数学 来源: 题型:
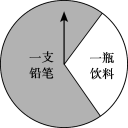
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点D.
于点D.
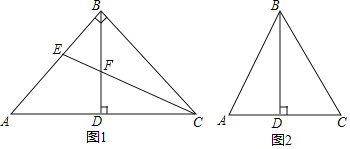
(1)如图1,当![]() 时,若CE平分
时,若CE平分![]() ,交AB于点E,交BD于点F.
,交AB于点E,交BD于点F.
①求证:![]() 是等腰三角形;
是等腰三角形;
②求证:![]() ;
;
(2)点E在AB边上,连接CE.若![]() ,在图2中补全图形,判断
,在图2中补全图形,判断![]() 与
与![]() 之间的数量关系,写出你的结论,并写出求解
之间的数量关系,写出你的结论,并写出求解![]() 与
与![]() 关系的思路.
关系的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com