
����Ŀ�����Ƕ��壺��![]() ��������
��������![]() �İ��溯�������磺
�İ��溯�������磺![]() ����
����![]() �İ��溯�������ν����ѧϰ������һ����Ҫ���������ڶ��κ���
�İ��溯�������ν����ѧϰ������һ����Ҫ���������ڶ��κ���![]() ��
��![]() �ij�����������
�ij�����������![]() �ں���
�ں���![]() ��ͼ���ϣ���㣨
��ͼ���ϣ���㣨![]() ��
��![]() ��Ҳ����ͼ���ϣ��������ĽǶȿ���֪������ͼ�����
��Ҳ����ͼ���ϣ��������ĽǶȿ���֪������ͼ�����![]() ��Գƣ�����������⣺
��Գƣ�����������⣺
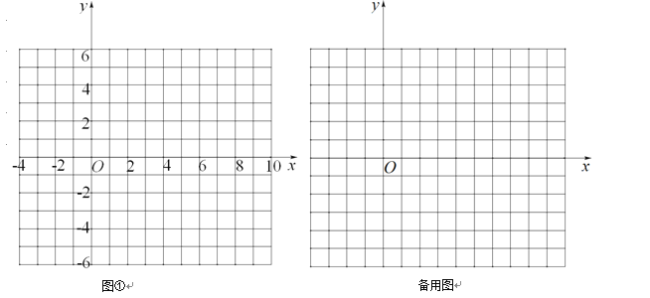
��1��![]() ��ͼ����� ��Գƣ�
��ͼ����� ��Գƣ�
��2����ֱ��д������![]() �İ��溯���ı���ʽ ��
�İ��溯���ı���ʽ ��
������ͼ����ʾ��ƽ��ֱ������ϵ�л���![]() �İ��溯���Ĵ���ͼ��
�İ��溯���Ĵ���ͼ��
��3����ֱ��![]() ��
��![]() �İ��溯��ͼ����
�İ��溯��ͼ����![]() ��
��![]() ���㣨��A�ڵ�B���Ϸ���������
���㣨��A�ڵ�B���Ϸ���������![]() ��
��![]() ���ҡ�ABO�����Ϊ12����
���ҡ�ABO�����Ϊ12����![]() ��ֵ��
��ֵ��
��4����ֱ��![]() ��
��![]() ��ƽ����y�ᣩ��
��ƽ����y�ᣩ��![]() ��
��![]() �ij������İ��溯��ͼ����
�ij������İ��溯��ͼ����![]() ��
��![]() ���㣨��
���㣨��![]() ��
��![]() �ֱ��ڵ�һ�������ޣ�����
�ֱ��ڵ�һ�������ޣ�����![]() ������
������![]() ��
��![]() �����������Ļ��Ƿ�Ϊ����������ǣ������֤����������ǣ���˵�����ɣ�
�����������Ļ��Ƿ�Ϊ����������ǣ������֤����������ǣ���˵�����ɣ�
���𰸡���1������![]() ��Գƣ���2����
��Գƣ���2����![]() ���������������3��
���������������3��![]() ����4��
����4��![]() ��
��![]() �����������֮��Ϊ���������ɼ���⣮
�����������֮��Ϊ���������ɼ���⣮
��������
��1������![]() �ص㣬�������
�ص㣬�������![]() ��ͼ�����
��ͼ�����![]() ��Գƣ�
��Գƣ�
��2�����ݰ��溯���Ķ��壬����д���𰸣�
��3�������ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ⷽ����
���ⷽ����![]() ���ú�k��ʽ�ӱ�ʾy1,y2��������ʾ��
���ú�k��ʽ�ӱ�ʾy1,y2��������ʾ��![]() ��������ABO�����Ϊ12�����
��������ABO�����Ϊ12�����![]() ���������k��
���������k��
��4����![]() ��
��![]() ���ֱ��
���ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() �ᣬ����ֱ�Ϊ
�ᣬ����ֱ�Ϊ![]() ����֤��
����֤��![]() ��
��![]() ����A��B�������ʾ���������
����A��B�������ʾ���������![]() �İ��溯����ϵʽ���õ�
�İ��溯����ϵʽ���õ�![]() ��
��![]() �����������Ļ�Ϊ
�����������Ļ�Ϊ![]() ������ý⣮
������ý⣮
�⣺��1��![]() ��
��![]() ��ͼ���ϣ���
��ͼ���ϣ���![]()
![]() ����ͼ���ϣ�����
����ͼ���ϣ�����![]() ��ͼ����� ����
��ͼ����� ����![]() ��Գƣ�
��Գƣ�
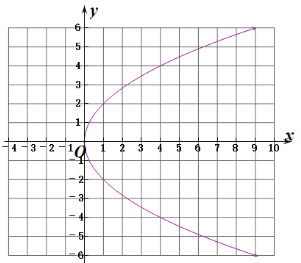
��2����![]() ��ͼ����ͼ��
��ͼ����ͼ��
��3����![]() �൱
�൱![]() ʱ
ʱ![]() ��
��
��ֱ�߽�![]() ���ڵ�
���ڵ�![]() ��
��![]()
��![]() ��
��![]() ����������
����������![]()
��![]() ��
��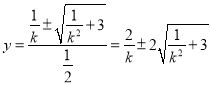
��![]() �֡�
�֡�![]()
��![]()
��![]() ��
��![]()
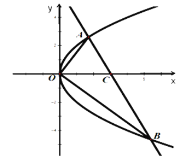
��4��![]() ��
��![]() �����������֮��Ϊ����
�����������֮��Ϊ����
�ߵ�![]() ����
����![]() ͼ���ϣ���
ͼ���ϣ���![]() ��
��![]() �ֱ��ڵ�һ��������
�ֱ��ڵ�һ��������
�����![]() ��
��![]()
�ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() �ᣬ����ֱ�Ϊ
�ᣬ����ֱ�Ϊ![]()
�֡�![]() ��
��![]()
��![]() ��
��![]()
��![]() ��
��![]()
��![]()
��![]() ������
Ϊ������![]() �����������֮��Ϊ������
�����������֮��Ϊ������


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
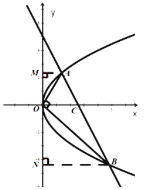
����Ŀ��ij�羰����Ϊ�˷����ο͵���ɽ�����ƻ���ɽ��A�㵽ɽ��C�����۹��³�����ʱ��A��۲�C�������Ϊ45�ȣ�ʩ���龭��ʵ�ؿ����Ϊ�˰�ȫ���������۹��³��ĸ�����ΪAD��CD���Σ�D���ǰ�ɽ���Ͼ������AB30��һ��֧�㣬��A��۲�D�������Ϊ30������D��۲�ɽ��C�������Ϊ75��������ͨ���Լ�ѧ����֪ʶ���������ɽ�ĸ߶�BCԼΪ�����ף���������������������õ������ݣ�![]() ��1.73��sin75���0.96��cos75���0.26��tan75���3.73��
��1.73��sin75���0.96��cos75���0.26��tan75���3.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ�����Ľ���ʱ�ڣ�����������������裬������Ƥ�����������������ȣ�����������������ţ�Ϊ�˽����������������������ͬ�����ij����С����������˲�������(�����ʾ�����)�������ݵ����������������в�������ͳ��ͼ��
�����ʾ�
������������ѡ��һ��? (ÿ��ֻѡһ��)
A.�������������������������ÿ�����������
B.�������ֽṹ����������������
C.ѡ��������Ʒ�֣����ƹ���ֲ��
D.������ע����������أ��������������
E.������
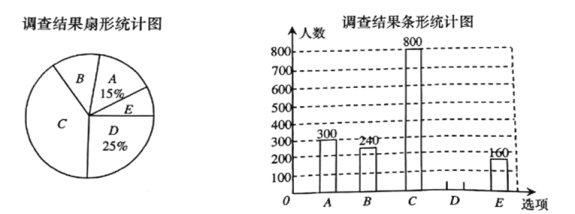
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�������![]() ��Բ�ĽǶ�����
��Բ�ĽǶ�����
��2����ȫ����ͳ��ͼ��
��3��������Լ��![]() ���ˣ��������ͬ��ѡ��������Ʒ�֣����ƹ���ֲ����������
���ˣ��������ͬ��ѡ��������Ʒ�֣����ƹ���ֲ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǽ�![]() ��
��![]() ��Ϊһ�ԡ���żʽ������Ϊ
��Ϊһ�ԡ���żʽ������Ϊ![]()
![]() �����Թ��조��żʽ���ٽ�����˿�����Ч�Ľ�
�����Թ��조��żʽ���ٽ�����˿�����Ч�Ľ�![]() ��
��![]() �еġ�
�еġ�![]() ��ȥ��.���Ƕ��θ�ʽ�������������⣺��
��ȥ��.���Ƕ��θ�ʽ�������������⣺��![]() ��
��![]()
![]() ����������ͨ�����ӣ���ĸͬ����һ��ʽ�Ӱѷ�ĸ�еĸ��Ż�ȥ��Ѹ����еķ�ĸ��ȥ��������ĸ������.�������ϲ��ϣ����Ⲣ���ò����ṩ�ķ���������������⣺
����������ͨ�����ӣ���ĸͬ����һ��ʽ�Ӱѷ�ĸ�еĸ��Ż�ȥ��Ѹ����еķ�ĸ��ȥ��������ĸ������.�������ϲ��ϣ����Ⲣ���ò����ṩ�ķ���������������⣺
��1���Ƚϴ�С![]() ________
________![]() ���á�
���á�![]() ������
������![]() ����
����![]() ����գ���
����գ���
��2����֪![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
��3�����㣺![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУȫ��ѧ�������μ��װ��Ĵ��ƾ����Ϊ�˽�������������ȡ�˲���ѧ���������ǵľ���������ͳ�ƣ����Ƴ�������������ͳ��ͼ��ͳ��ͼ��ÿ�麬��Сֵ���������ֵ����������ͼ����Ϣ����������⣺
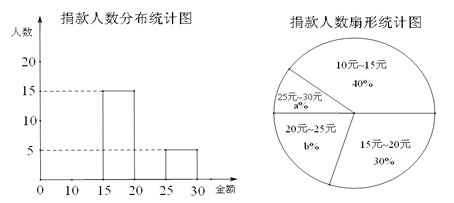
��1���������ȡ��ѧ��������
��2����գ�(ֱ�����) �١�20Ԫ��25Ԫ�����ֶ�Ӧ��Բ�ĽǶ���Ϊ ����
��������λ������ ��(���Χ)��
��3������У����ѧ��2100�ˣ������ȫУ������20Ԫ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��������㷨�����κ���y��ax2+bx+c��a��0����ͼ��ʱ����ȡ�Ա���x��һЩֵ���������Ӧ�ĺ���ֵy�����±���ʾ��
x | �� | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | ��3 | 0 | ��1 | 0 | 3 | �� |
���ţ��������ʱ���֣���������һ�����ݼ����������������һ�������ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ģ�߳��ƻ��������Ϊ4���ܳ�Ϊm�ľ���ģ�ߣ�����m��ȡֵ��Χ��С���Ѿ��������������ķ���������������ֳ��Դ���ͼ�����ĽǶȽ���̽�����������£�
��1����������ģ��
������������ߵij��ֱ�Ϊx��y���ɾ��ε����Ϊ4����xy=4����![]() �����ܳ�Ϊm����2��x+y��=m����y=-x+
�����ܳ�Ϊm����2��x+y��=m����y=-x+![]() ������Ҫ��ģ�x��y��Ӧ����������ͼ���ڵ� �����ڽ�������꣮
������Ҫ��ģ�x��y��Ӧ����������ͼ���ڵ� �����ڽ�������꣮
��2����������ͼ��
����![]() ��x��0����ͼ����ͼ��ʾ��������y=-x+
��x��0����ͼ����ͼ��ʾ��������y=-x+![]() ��ͼ�����ֱ��y=-xƽ�Ƶõ�������ͬһֱ������ϵ��ֱ�ӻ���ֱ��y=-x��
��ͼ�����ֱ��y=-xƽ�Ƶõ�������ͬһֱ������ϵ��ֱ�ӻ���ֱ��y=-x��

��3��ƽ��ֱ��y=x���۲캯��ͼ��
��ֱ��ƽ�ƹ����У������������Щ�������д�������������Ӧ���ܳ�m��ȡֵ��Χ��
��4���ó����� �������������Ϊ4�ľ���ģ�ߣ����ܳ�m��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
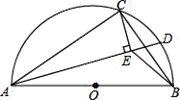
����Ŀ����ͼ��![]() �ǰ�Բ
�ǰ�Բ![]() ��ֱ����
��ֱ����![]() ��
��![]() .
.![]() �ǻ�
�ǻ�![]() �ϵ�һ������(���˵�
�ϵ�һ������(���˵�![]() �������˵�
�������˵�![]() )������
)������![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ���ڵ�
���ڵ�![]() �ƶ��Ĺ����У�
�ƶ��Ĺ����У�![]() ��ȡֵ��Χ��( )
��ȡֵ��Χ��( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
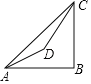
����Ŀ��(2014ɽ���Ͳ�)��ͼ���ı���ABCD�У�AC��BD��BD�ڵ�E����F��M�ֱ���AB��BC���е㣬BNƽ����ABE��AM�ڵ�N��AB��AC��BD������MF��NF��
(1)�ж���BMN����״����֤����Ľ��ۣ�
(2)�ж���MFN����BDC֮��Ĺ�ϵ����˵�����ɣ�
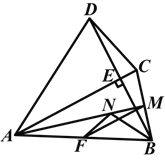
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com