
����Ŀ��Ϊ�˴���ȫ�µ�У�Ļ���Χ����һ����֯ѧ����չ�����Ķ�����ѧ���ڷḻ��ʵ��麣�У�����֪ʶԴ����ĸ������ѧ������ijУ����չ���뾭��Ϊ�ѡ�������Ϊ�顱���Ķ�����ǰ�Ա�Уѧ�������ˡ�����ϲ����ͼ�����ͣ�ֻдһ���������������飬�������ͳ�����£�
�����������Ϣ����������⣺
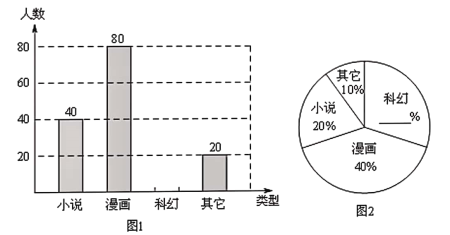
��1����У�Զ�����ѧ�������˳������飿
��2���뽫ͼ1��ͼ2�������������������ͳ��ͼ��С˵����Ӧ��Բ�ĽǶ�����
��3����֪��У����ѧ��1600�ˣ������������ݹ���ȫУѧ������ϲ��С˵����ԼΪ�����ˣ�
���𰸡���1��200����2��ͼ1��ͼ2��������![]() ����3��720
����3��720
��������
��1����ϲ��С˵����������ϲ��С˵��������ռ�İٷֱȣ����������������
��2��������������ȥ��������������������ϲ���ƻõ������������ðٷֱȵ��������ϲ���ƻõİٷֱȣ��ݴ˿ɲ���������ͼ1��ͼ2������С˵��ռ�İٷֱȳ���![]() �����ɵõ�����ͳ��ͼ��С˵����Ӧ��Բ�ĽǶ�����
�����ɵõ�����ͳ��ͼ��С˵����Ӧ��Բ�ĽǶ�����
��3������ȫУѧ������������С˵��ռ�İٷֱȣ����ɵõ�ȫУѧ������ϲ��С˵������
��1��![]() ��������
��������
�𣺸�У��200��ѧ�������˳������飮
��2��ϲ���ƻõ�����Ϊ��![]() ��������
��������
ϲ���ƻõ�������ռ�İٷֱ�Ϊ��![]() ��
��
����������ͼ1��ͼ2������ʾ��
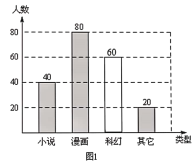
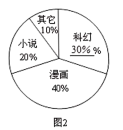
����ͳ��ͼ��С˵����Ӧ��Բ�ĽǶ���Ϊ��![]() ��
��
��3��![]() ��������
��������
��ȫУѧ������ϲ��С˵����ԼΪ720����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��һ�����ʵ����У�ͨ����ij���߲���1�·���7�·ݵ��г��������ͳ�Ʒ�����ó����¹��ɣ� �ٸ��߲˵����ۼ�P����λ��Ԫ/ǧ�ˣ���ʱ��x����λ���·ݣ������ϵ��P=9��x
�ڸ��߲˵�ƽ���ɱ�y����λ��Ԫ/ǧ�ˣ���ʱ��x����λ���·ݣ�������κ�����ϵy=ax2+bx+10����֪4�·ݵ�ƽ���ɱ�Ϊ2Ԫ/ǧ�ˣ�6�·ݵ�ƽ���ɱ�Ϊ1Ԫ/ǧ�ˣ�
��1����ö��κ����Ľ���ʽ��
��2��������С��ͳ�ƵĽ��ۣ�������߲��ڵڼ��·ݵ�ƽ������L����λ��Ԫ/ǧ�ˣ�������ƽ�������Ƕ��٣���ע��ƽ������=���ۼ۩�ƽ���ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ6cm��������ABCD�У���E��F��G��H�ֱ�ӵ�A��B��C��Dͬʱ����������1cm/s���ٶ����B��C��D��A�����˶�������E�����Bʱ���ĸ���ͬʱֹͣ�˶������˶������У����˶�ʱ��Ϊsʱ���ı���EFGH�������С������Сֵ��cm2 �� 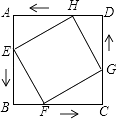
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1��AB��CD����PAB=130�㣬��PCD=120�㣮����APC������
С���Ľ���˼·�ǣ���ͼ2����P��PE��AB��ͨ��ƽ�������ʣ��ɵ���APC=50��+60��=110�㣮
����Ǩ�ƣ�
��1����ͼ3��AD��BC����P������OM���˶�������P��A��B����֮���˶�ʱ����ADP=��������BCP=���£����ж���CPD������������֮���к�������ϵ����˵�����ɣ�


��2���ڣ�1���������£������P��A��B��������˶�ʱ����P���A��B��O���㲻�غϣ�������ֱ��д����CPD�����������¼��������ϵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������Լ��ˮ��ij�о����Ծ�����ˮ�շ�ʵ�С����ݼۡ�������ÿ����ˮ��������15��ʱ������15�֣������û������շѣ���ÿ����ˮ������15��ʱ����������ÿ�ֲ����г����շѣ�С����4��5�·ݵ���ˮ�����շ�������±���
�·� | ��ˮ�����֣� | ˮ�ѣ�Ԫ�� |
4 | 22 | 51 |
5 | 20 | 45 |
��1�������ÿ��ˮ�Ļ����ۺ��г��ۣ�
��2����ÿ����ˮ��Ϊn�֣�Ӧ��ˮ��ΪmԪ����д��m��n֮��ĺ�����ϵʽ��
��3��С����6�·ݵ���ˮ��Ϊ26�֣�������Ҫ��ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿ��С�����εı߳�����1�ķ���ֽ�У����߶�AB���߶�CD����A��B��C��D�Ķ˵㶼��С�����εĶ����ϣ�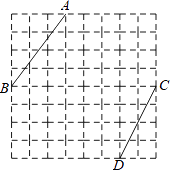
��1�����ڷ���ֽ�л���һ�����߶�ABΪһ�ߵ�����ABEF�����������εĸ����������С�����εĶ����ϣ����������Ϊ20��
���ڷ���ֽ����CDΪ�ױ�������������CDK����K��С�����εĶ����ϣ��ҡ�CDK�����Ϊ5��
��2���ڣ�1���������£�����BK����ֱ��д���߶�BK�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=�� ![]() x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��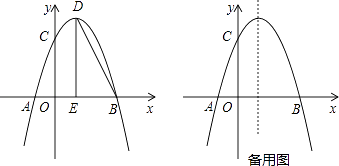
�����������ߵĽ���ʽ����D�����ꣻ
����F���������ϵĶ��㣬����FBA=��BDEʱ�����F�����ꣻ
��������M���������ϵĶ��㣬����M��MN��x���������߽��ڵ�N����P��x���ϣ���Q������ƽ���ڣ����߶�MNΪ�Խ�����������MPNQ����д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
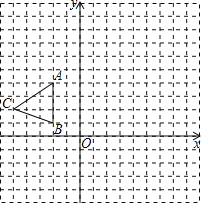
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC�������������ֱ�ΪA(��2��4)��B(��2��1)��C(��5��2)��
(1)�뻭����ABC����x��ԳƵ���A1B1C1��
(2)����A1B1C1����������ĺ�������������ͬʱ�ˣ�2���õ���Ӧ�ĵ�A2��B2��C2���뻭����A2B2C2��
(3)д����A1B1C1���������A2B2C2�������(��д�����̣�ֱ��д�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��:
(1)��֪һ������![]() ,������ӡ���ĸͬʱ����1,������ֵ�������Ǽ�С?��˵���������.
,������ӡ���ĸͬʱ����1,������ֵ�������Ǽ�С?��˵���������.
(2)��������![]() �з��Ӻͷ�ĸͬʱ����2,3,��,k(����k>0),������?
�з��Ӻͷ�ĸͬʱ����2,3,��,k(����k>0),������?
(3)����������Ľ��۽������������:
����ѧ�涨:����סլ�����������С�ڵذ����,�����ɹ��,���������ذ�����ı�Ӧ��С��10%,���������ֵԽ��,סլ�IJɹ�����Խ��,��:ͬʱ������ȵĴ�������͵ذ����,סլ�IJɹ������DZ����,���DZ仵��?��˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com