
【题目】甲、乙两车从![]() 城出发匀速行驶至
城出发匀速行驶至![]() 城在整个行驶过程中,甲乙两车离开
城在整个行驶过程中,甲乙两车离开![]() 城的距离
城的距离![]() 与甲车行驶的时间
与甲车行驶的时间![]() 之间的函数关系如图所示下列说法错误的是( )
之间的函数关系如图所示下列说法错误的是( )
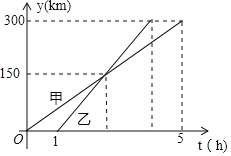
甲、乙两车从AA城出发匀速行驶至BB城在整个行驶过程中,甲乙两车离开AA城的距离y(km)ykm与甲车行驶的时间t(h)th之间的函数关系如图所示下列说法错误的是()
A.![]() ,
,![]() 两城相距
两城相距![]() 千米
千米
B.乙车比甲车晚出发![]() 小时,却早到
小时,却早到![]() 小时
小时
C.乙车出发后![]() 小时追上甲车
小时追上甲车
D.在一车追上另一车之前,当两车相距![]() 千米时,
千米时,![]()
【答案】D
【解析】
由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,进而判断,再令两函数解析式的差为40,可求得t,可得出答案.
由图象可知A、B两城市之间的距离为300km,故A正确;
设甲车离开A城的距离y与t的关系式为![]() ,
,
把(5,300)代入可求得![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() ,可得:
,可得:![]() ,
,
设乙车离开A城的距离y与t的关系式为![]() ,
,
把(1,0)和(2.5,150)代入可得![]()
解得:![]()
∴![]() ,
,
令![]() 可得:
可得:![]() ,解得
,解得![]() ,
,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5-1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故B正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故C正确;
令|![]() |
|![]() ,可得
,可得![]() ,即
,即![]() ,
,
当![]() 时,可解得
时,可解得![]() ,
,
当![]() 时,可解得
时,可解得![]() (不合题意,舍去),
(不合题意,舍去),
又当![]() 时,
时,![]() ,此时乙还没出发,
,此时乙还没出发,
当![]() 时(不合题意,舍去);
时(不合题意,舍去);
综上可知当t的值为当![]() 或
或![]() 时,两车相距40千米,故D不正确;
时,两车相距40千米,故D不正确;
故选:D.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
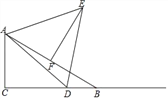
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A在第一象限,点A,B关于y轴对称.
(1)若A(1,3),写出点B的坐标并在直角坐标系中标出.
(2)若A(a,b),且△AOB的面积为a2,求点B的坐标(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南开中学校庆78周年之际,由学生处和美术教研组共同策划、组织了“南开中学校园明信片设计大赛”。获得此次设计大赛组织一等奖的![]() 、
、![]() 、
、![]() 、
、![]() 四个班级一共有75件作品获奖,已知
四个班级一共有75件作品获奖,已知![]() 班参赛作品的获奖率为30%,
班参赛作品的获奖率为30%,![]() 班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题:
班参赛作品的获奖率为40%。请结合两幅统计图所提供的信息,解决下列问题: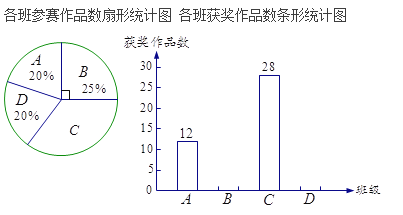
(1)四个班级一共选送了多少件作品参赛,获奖率最高的班级是哪个班;
(2)请将条形统计图补充完整;
(3)![]() 班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外
班的小欣和小怡同学在本次大赛中荣获个人一等奖,此外![]() 、
、![]() 两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
两班各有一名同学荣获个人一等奖。南开中学校友会准备从这4名同学的作品中任选两件,制作成新年贺卡送给老校友。请用列表法或画树状图的方法求出这两件作品分别来自不同班级,且其中一件是小欣或小怡作品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个横截面是正方形的长方体平均截成![]() 段后,每段长
段后,每段长![]() 分米,这样表面积就增加了
分米,这样表面积就增加了![]() 平方分米,原来长方体的表面积是________平方分米,体积是________立方分米.
平方分米,原来长方体的表面积是________平方分米,体积是________立方分米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AD=2AB,
ABCD中,AD=2AB,![]() ,垂足
,垂足![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() :③
:③![]() ;④
;④![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
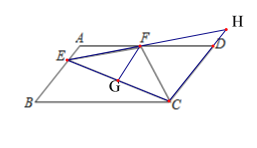
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个分式的和为![]() (
(![]() 为正整数),则称这两个分式互为“
为正整数),则称这两个分式互为“![]() 阶分式”,例如分式
阶分式”,例如分式![]() 与
与![]() 互为“3阶分式”.
互为“3阶分式”.
(1)分式![]() 与 互为“5阶分式”;
与 互为“5阶分式”;
(2)设正数![]() 互为倒数,求证:分式
互为倒数,求证:分式![]() 与
与![]() 互为“2阶分式”;
互为“2阶分式”;
(3)若分式![]() 与
与![]() 互为“1阶分式”(其中
互为“1阶分式”(其中![]() 为正数),求
为正数),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
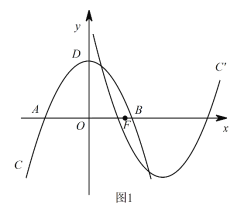
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com