
【题目】如图,在![]() ABCD中,AD=2AB,
ABCD中,AD=2AB,![]() ,垂足
,垂足![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() :③
:③![]() ;④
;④![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
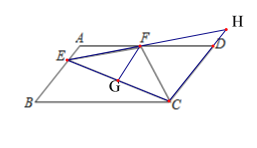
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由点F是AD的中点,结合![]() ABCD的性质,得FD=CD,即可判断①;先证AEFDHF,再证ECH是直角三角形,即可判断②;由EF=HF,得
ABCD的性质,得FD=CD,即可判断①;先证AEFDHF,再证ECH是直角三角形,即可判断②;由EF=HF,得![]() ,由
,由![]() ,CE⊥CD,结合三角形的面积公式,即可判断③;设∠AEF=x,则∠H=x,根据直角三角形的性质,得∠FCH=∠H=x,由FD=CD,∠DFC=∠FCH=x,由FG∥CD∥AB,得∠AEF=∠EFG=x,由EF=CF,∠EFG=∠CFG=x,进而得到
,CE⊥CD,结合三角形的面积公式,即可判断③;设∠AEF=x,则∠H=x,根据直角三角形的性质,得∠FCH=∠H=x,由FD=CD,∠DFC=∠FCH=x,由FG∥CD∥AB,得∠AEF=∠EFG=x,由EF=CF,∠EFG=∠CFG=x,进而得到![]() ,即可判断④.
,即可判断④.
∵点F是AD的中点,
∴2FD=AD,
∵在![]() ABCD中,AD=2AB,
ABCD中,AD=2AB,
∴FD=AB=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠BCF,
∴∠DCF=∠BCF,即:![]() ,
,
∴①正确;
∵AB∥CD,
∴∠A=∠FDH,∠AEF=∠H,
又∵AF=DF,
∴AEFDHF(AAS),
∴EF=HF,
∵![]() ,
,
∴CE⊥CD,即:ECH是直角三角形,
∴![]() =
=![]() EH,
EH,
∴②正确;
∵EF=HF,
∴![]()
∵![]() ,CE⊥CD,垂足
,CE⊥CD,垂足![]() 在线段
在线段![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴③错误;
设∠AEF=x,则∠H=x,
∵在RtECH中,CF=FH=EF,
∴∠FCH=∠H=x,
∵FD=CD,
∴∠DFC=∠FCH=x,
∵点F,G分别是EH,EC的中点,
∴FG∥CD∥AB,
∴∠AEF=∠EFG=x,
∵EF=CF,
∴∠EFG=∠CFG=x,
∴∠DFE=∠DFC+∠EFG+∠CFG=3x,
∴![]() .
.
∴④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别以
分别以![]() 、
、![]() 的速度从点
的速度从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 向点
向点![]() 移动.
移动.

![]() 若点
若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 随点
随点![]() 的停止而停止移动,点
的停止而停止移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过多长时间
同时出发,问经过多长时间![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ?
?
![]() 若点
若点![]() 沿着
沿着![]() 移动,点
移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 移动到点
移动到点![]() 停止时,点
停止时,点![]() 随点
随点![]() 的停止而停止移动,试探求经过多长时间
的停止而停止移动,试探求经过多长时间![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 城出发匀速行驶至
城出发匀速行驶至![]() 城在整个行驶过程中,甲乙两车离开
城在整个行驶过程中,甲乙两车离开![]() 城的距离
城的距离![]() 与甲车行驶的时间
与甲车行驶的时间![]() 之间的函数关系如图所示下列说法错误的是( )
之间的函数关系如图所示下列说法错误的是( )
甲、乙两车从AA城出发匀速行驶至BB城在整个行驶过程中,甲乙两车离开AA城的距离y(km)ykm与甲车行驶的时间t(h)th之间的函数关系如图所示下列说法错误的是()
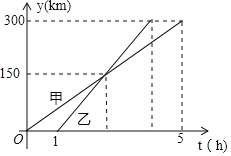
A.![]() ,
,![]() 两城相距
两城相距![]() 千米
千米
B.乙车比甲车晚出发![]() 小时,却早到
小时,却早到![]() 小时
小时
C.乙车出发后![]() 小时追上甲车
小时追上甲车
D.在一车追上另一车之前,当两车相距![]() 千米时,
千米时,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 以每秒1个单位长度的速度从
以每秒1个单位长度的速度从![]() 点出发,沿
点出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒2个单位长度的速度从点
同时以每秒2个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() ______秒时,以点
______秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
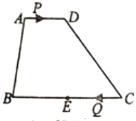
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品的原料提价,因而厂家决定对产品提价,现有三种方案:
方案(一):第一次提价![]() ,第二次提价
,第二次提价![]() ;
;
方案(二):第一次提价![]() ,第二次提价
,第二次提价![]() ;
;
方案(三):第一、二次提价均为![]() ;
;
其中![]() ,
,![]() 是不相等的正数.
是不相等的正数.
有以下说法:
①方案(一)、方案(二)提价一样;
②方案(一)的提价也有可能高于方案(二)的提价;
③三种方案中,以方案(三)的提价最多;
④方案(三)的提价也有可能会低于方案(一)或方案(二)的提价.
其中正确的有( )
A.②③B.①③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(1)求反比例函数的解析式;
(2)求△OEF的面积;
(3)设直线EF的解析式为y=k2x+b,请结合图象直接写出不等式k2x+b>![]() 的解集.
的解集.
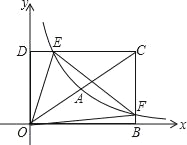
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(![]() ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com