
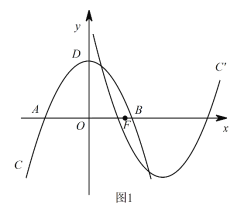
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпCЃКy=ax2+bx+cгыxжсЯрНЛгкAЃЌBСНЕуЃЌЖЅЕуЮЊD(0ЃЌ4)ЃЌAB=4![]() ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
(1)ЧѓХзЮяЯпCЕФКЏЪ§БэДяЪНЃЛ
(2)ШєХзЮяЯпC/гыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
(3)ШчЭМ2ЃЌPЪЧЕквЛЯѓЯоФкХзЮяЯпCЩЯвЛЕуЃЌЫќЕНСНзјБъжсЕФОрРыЯрЕШЃЌЕуPдкХзЮяЯпC/ЩЯЕФЖдгІЕуP/ЃЌЩшMЪЧCЩЯЕФЖЏЕуЃЌNЪЧC/ЩЯЕФЖЏЕуЃЌЪдЬНОПЫФБпаЮPMP/NФмЗёГЩЮЊе§ЗНаЮЃПШєФмЃЌЧыжБНгаДГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ2ЃМmЃМ
ЃЛЃЈ2ЃЉ2ЃМmЃМ![]() ЃЛЃЈ3ЃЉm=6Лђm=
ЃЛЃЈ3ЃЉm=6Лђm=![]() Љ3ЃЎ
Љ3ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉгЩЬтвтХзЮяЯпЕФЖЅЕуCЃЈ0ЃЌ4ЃЉЃЌAЃЈ![]() ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌАбAЃЈ
ЃЌАбAЃЈ![]() ЃЌ0ЃЉДњШыПЩЕУa=
ЃЌ0ЃЉДњШыПЩЕУa=![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩЬтвтХзЮяЯпCЁфЕФЖЅЕузјБъЮЊЃЈ2mЃЌЉ4ЃЉЃЌЩшХзЮяЯпCЁфЕФНтЮіЪНЮЊ![]() ЃЌгЩ
ЃЌгЩ ЃЌЯћШЅyЕУЕН
ЃЌЯћШЅyЕУЕН![]() ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга
ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга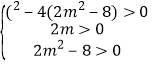 ЃЌНтВЛЕШЪНзщМДПЩНтОіЮЪЬтЃЛ
ЃЌНтВЛЕШЪНзщМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЧщаЮ1ЃЌЫФБпаЮPMPЁфNФмГЩЮЊе§ЗНаЮЃЎзїPEЁЭxжсгкEЃЌMHЁЭxжсгкHЃЎгЩЬтвтвзжЊPЃЈ2ЃЌ2ЃЉЃЌЕБЁїPFMЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЦГіPF=FMЃЌЁЯPFM=90ЁуЃЌвзжЄЁїPFEЁеЁїFMHЃЌПЩЕУPE=FH=2ЃЌEF=HM=2ЉmЃЌПЩЕУMЃЈm+2ЃЌmЉ2ЃЉЃЌРэгЩД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛЧщаЮ2ЃЌШчЭМЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЌЗЈПЩЕУMЃЈmЉ2ЃЌ2ЉmЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтХзЮяЯпЕФЖЅЕуCЃЈ0ЃЌ4ЃЉЃЌAЃЈ![]() ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌАбAЃЈ
ЃЌАбAЃЈ![]() ЃЌ0ЃЉДњШыПЩЕУa=
ЃЌ0ЃЉДњШыПЩЕУa=![]() ЃЌЁрХзЮяЯпCЕФКЏЪ§БэДяЪНЮЊ
ЃЌЁрХзЮяЯпCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтХзЮяЯпCЁфЕФЖЅЕузјБъЮЊЃЈ2mЃЌЉ4ЃЉЃЌЩшХзЮяЯпCЁфЕФНтЮіЪНЮЊ![]() ЃЌгЩ
ЃЌгЩ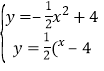 ЃЌЯћШЅyЕУЕН
ЃЌЯћШЅyЕУЕН![]() ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга
ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга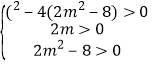 ЃЌНтЕУ2ЃМmЃМ
ЃЌНтЕУ2ЃМmЃМ![]() ЃЌЁрТњзуЬѕМўЕФmЕФШЁжЕЗЖЮЇЮЊ2ЃМmЃМ
ЃЌЁрТњзуЬѕМўЕФmЕФШЁжЕЗЖЮЇЮЊ2ЃМmЃМ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉНсТлЃКЫФБпаЮPMPЁфNФмГЩЮЊе§ЗНаЮЃЎ
РэгЩЃК1ЧщаЮ1ЃЌШчЭМЃЌзїPEЁЭxжсгкEЃЌMHЁЭxжсгкHЃЎ
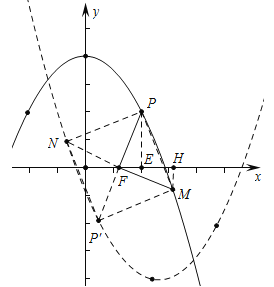
гЩЬтвтвзжЊPЃЈ2ЃЌ2ЃЉЃЌЕБЁїPFMЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЁрPF=FMЃЌЁЯPFM=90ЁуЃЌвзжЄЁїPFEЁеЁїFMHЃЌПЩЕУPE=FH=2ЃЌEF=HM=2ЉmЃЌЁрMЃЈm+2ЃЌmЉ2ЃЉЃЌЁпЕуMдк![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌНтЕУm=
ЃЌНтЕУm=![]() Љ3ЛђЉ
Љ3ЛђЉ![]() Љ3ЃЈЩсЦњЃЉЃЌЁрm=
Љ3ЃЈЩсЦњЃЉЃЌЁрm=![]() Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
ЧщаЮ2ЃЌШчЭМЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЌЗЈПЩЕУMЃЈmЉ2ЃЌ2ЉmЃЉЃЌАбMЃЈmЉ2ЃЌ2ЉmЃЉДњШы![]() жаЃЌ
жаЃЌ![]() ЃЌНтЕУm=6Лђ0ЃЈЩсЦњЃЉЃЌЁрm=6ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
ЃЌНтЕУm=6Лђ0ЃЈЩсЦњЃЉЃЌЁрm=6ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
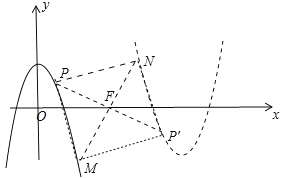
злЩЯЫљЪіЃКm=6Лђm=![]() Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНГЕДг![]() ГЧГіЗЂдШЫйааЪЛжС
ГЧГіЗЂдШЫйааЪЛжС![]() ГЧдкећИіааЪЛЙ§ГЬжаЃЌМзввСНГЕРыПЊ
ГЧдкећИіааЪЛЙ§ГЬжаЃЌМзввСНГЕРыПЊ![]() ГЧЕФОрРы
ГЧЕФОрРы![]() гыМзГЕааЪЛЕФЪБМф
гыМзГЕааЪЛЕФЪБМф![]() жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
МзЁЂввСНГЕДгAAГЧГіЗЂдШЫйааЪЛжСBBГЧдкећИіааЪЛЙ§ГЬжаЃЌМзввСНГЕРыПЊAAГЧЕФОрРыy(km)ykmгыМзГЕааЪЛЕФЪБМфt(h)thжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЃЉ
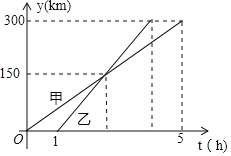
A.![]() ЃЌ
ЃЌ![]() СНГЧЯрОр
СНГЧЯрОр![]() ЧЇУз
ЧЇУз
B.ввГЕБШМзГЕЭэГіЗЂ![]() аЁЪБЃЌШДдчЕН
аЁЪБЃЌШДдчЕН![]() аЁЪБ
аЁЪБ
C.ввГЕГіЗЂКѓ![]() аЁЪБзЗЩЯМзГЕ
аЁЪБзЗЩЯМзГЕ
D.дквЛГЕзЗЩЯСэвЛГЕжЎЧАЃЌЕБСНГЕЯрОр![]() ЧЇУзЪБЃЌ
ЧЇУзЪБЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
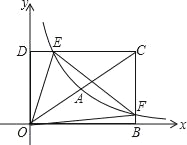
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮDOBCЕФЖЅЕуOгызјБъдЕужиКЯЃЌBЁЂDЗжБ№дкзјБъжсЩЯЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ4ЃЉЃЌЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЯпЖЮOCЕФжаЕуAЃЌНЛDCгкЕуEЃЌНЛBCгкЕуFЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЯпЖЮOCЕФжаЕуAЃЌНЛDCгкЕуEЃЌНЛBCгкЕуFЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїOEFЕФУцЛ§ЃЛ
ЃЈ3ЃЉЩшжБЯпEFЕФНтЮіЪНЮЊy=k2x+bЃЌЧыНсКЯЭМЯѓжБНгаДГіВЛЕШЪНk2x+bЃО![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХДКНкСйНќЃЌФГЖљЭЏгЮРжГЁЭЦГіСЫМзЁЂввСНжжЯћЗбПЈЃЌЩшЯћЗбДЮЪ§ЮЊ![]() ЪБЃЌЫљашЗбгУЮЊ
ЪБЃЌЫљашЗбгУЮЊ![]() дЊЃЌЧв
дЊЃЌЧв![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕШчЭМЫљЪО. ИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃЛ
ЕФКЏЪ§ЙиЯЕШчЭМЫљЪО. ИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃЛ
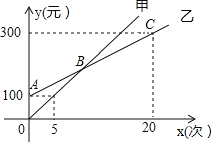
ЃЈ1ЃЉЗжБ№ЧѓГібЁдёетСНжжПЈЯћЗбЪБЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§БэДяЪН.
ЕФКЏЪ§БэДяЪН.
ЃЈ2ЃЉЧѓГі![]() ЕузјБъ.
ЕузјБъ.
ЃЈ3ЃЉбѓбѓАжАжзМБИ![]() дЊЧЎгУгкбѓбѓдкИУгЮРжГЁЯћЗбЃЌЧыЮЪбЁдёФФжжЯћЗбПЈЛЎЫуЃП
дЊЧЎгУгкбѓбѓдкИУгЮРжГЁЯћЗбЃЌЧыЮЪбЁдёФФжжЯћЗбПЈЛЎЫуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХЃЈ3ЃЉАрЁА2017ФъаТФъСЊЛЖЛсЁБжаЃЌгавЛИіУўНБгЮЯЗЃЌЙцдђШчЯТЃКга4еХжНХЦЃЌБГУцЖМЪЧЯВбђбђЭЗЯёЃЌе§Уцга2еХаІСГЁЂ2еХПоСГЃЎЯжНЋ4еХжНХЦЯДдШКѓБГУцГЏЩЯАкЗХЕНзРЩЯЃЌШЛКѓШУЭЌбЇШЅЗжНХЦЃЎ
ЃЈ1ЃЉЯжаЁЗМгавЛДЮЗХЦЛњЛсЃЌШєе§УцЪЧаІСГЕФОЭЛёНБЃЌе§УцЪЧПоСГЕФВЛЛёНБЃЎЫ§ДгжаЫцЛњЗПЊвЛеХжНХЦЃЌЧѓаЁЗМЛёНБЕФИХТЪЃЎ
ЃЈ2ЃЉШчЙћаЁЗМЁЂаЁУїЖМгаЗСНеХХЦЕФЛњЛсЃЎаЁЗМЯШЗвЛеХЃЌЗХЛиКѓдйЗвЛеХЃЛаЁУїЭЌЪБЗПЊСНеХжНХЦЃЎЫћУЧЗПЊЕФСНеХжНХЦжажЛвЊГіЯжвЛеХаІСГОЭЛёНБЃЎЫћУЧЛёНБЕФЛњЛсЯрЕШТ№ЃПЭЈЙ§ЪїзДЭМЗжЮіЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
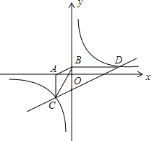
ЁОЬтФПЁПШчЭМЃЌвбжЊЫЋЧњЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() ЪЧЫЋЧњЯпЕкШ§ЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌЙ§Еу
ЪЧЫЋЧњЯпЕкШ§ЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЃЌЙ§Еу
жсЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЗжБ№ЮЊ
жсЃЌДЙзуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() Шє
Шє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
ЂйШєжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкИљОнЭМЯѓЃЌжБНгаДГі![]() ЪБ
ЪБ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЂлХаЖЯжБЯп![]() гы
гы![]() ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСННЈжўЮяABКЭCDЕФЫЎЦНОрРыЮЊ30УзЃЌШчЭМЫљЪОЃЌДгAЕуВтЕУЬЋбєТфЩНЪБЃЌЬЋбєЙтЯпACееЩфЕНABКѓЕФгАзгЧЁКУдкCDЕФЧННЧЪБЕФНЧЖШЁЯACB=60ЁуЃЌгжЙ§вЛЛсЖљЃЌЕБABЕФгАзге§КУЕНДяCDЕФТЅЖЅDЪБЕФНЧЖШЁЯADE=30ЁуЃЌDEЁЭABгкEЃЌдђНЈжўЮяCDЕФИпЪЧЖрЩйУзЃПЃЈ![]() Ёж1.732ЃЌНсЙћБЃСєСНЮЛгааЇЪ§зжЃЉ
Ёж1.732ЃЌНсЙћБЃСєСНЮЛгааЇЪ§зжЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИјЖЈЕФШ§ЕуФмШЗЖЈвЛИідВЕФЪЧЃЈ ЃЉ
A. ЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() МАСНИіЖЫЕу
МАСНИіЖЫЕу
B. НЧЕФЖЅЕуМАНЧЕФБпЩЯЕФСНЕу
C. Ш§НЧаЮЕФШ§ИіЖЅЕу
D. ОиаЮЕФЖдНЧЯпНЛЕуМАСНИіЖЅЕу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
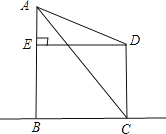
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯBACЃН90ЁуЃЌEЪЧBCЕФжаЕуЃЌADЁЮBCЃЌAEЁЮDCЃЌEFЁЭCDгкЕуF.
(1)ЧѓжЄЃКЫФБпаЮAECDЪЧСтаЮЃЛ
(2)ШєABЃН6ЃЌBCЃН10ЃЌЧѓEFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com