
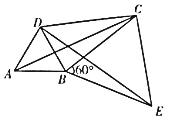
【题目】如图,![]() 和
和![]() 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.
(1)猜想AC与DE的数量关系,并说明理由。
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若![]() ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。
(3)设![]() ,
,![]() ,
,![]() 的面积分别是
的面积分别是![]() ,若
,若![]() ,试探究
,试探究![]() 与
与![]() 之间满足的等量关系。
之间满足的等量关系。
【答案】(1) AC=DE,理由见解析;(2)见解析;(3)![]()
【解析】
(1)证明△ABC≌△DBE即可得AC=DE;
(2)先证明△CDE为直角三角形, 得CE+CD=DE,再由CE=CB,DE=AC得CB+CD=AC,从而得出结论;
(3) 分别表示出S,S, S,再结合线段找出它们之间的关系.
(1)解: ∵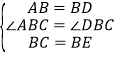 ,
,
∴△ABC≌△DBE(ASA),
∴AC=DE;
(2)证明: ∵∠DCE=90°,
∴△CDE为直角三角形,
∴CE+CD=DE,
又∵CE=CB,DE=AC,
∴CB+CD=AC,
∴四边形ABCD是勾股四边形;
(3)解:在等边△ABD与等边△BCE中,
S=![]() BD ,S=
BD ,S=![]() BC;
BC;
在直角三角形DBC中,S=![]() BD·BC,
BD·BC,
∵S·S=![]() (BD·BC) =
(BD·BC) =![]() (
(![]() (BD·BC) =
(BD·BC) =![]() S ,
S ,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在括号里填入理由:如图,
∵∠A=75°,∠1=75°(已知),
∴∠A=∠1 (___________________),
∴AM∥EN (______________________).
又∵∠2=∠1(对顶角相等),
∠3=105°(已知),
∴∠2+∠3=180°,
∴AB∥CD (______________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( ) 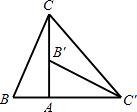
A.45°
B.30°
C.25°
D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,BC=AC,∠BCA=90°,P 为直线 AC 上一点,过 A作 AD⊥BP 于 D,交直线 BC 于 Q.
(1)如图 1,当 P 在线段 AC 上时,求证:BP=AQ.
(2)当 P 在线段 AC 的延长线上时,请在图 2 中画出图形,并求∠CPQ.
(3)如图 3,当 P 在线段 AC 的延长线上时,∠DBA= 时,AQ=2BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球.
某校羽毛球队需要购买![]() 副球拍和
副球拍和![]() 盒羽毛球
盒羽毛球![]() .
.
(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含![]() 的代数式表示;
的代数式表示;
(2)当![]() 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
(3)当![]() 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com