
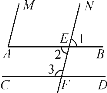
【题目】在括号里填入理由:如图,
∵∠A=75°,∠1=75°(已知),
∴∠A=∠1 (___________________),
∴AM∥EN (______________________).
又∵∠2=∠1(对顶角相等),
∠3=105°(已知),
∴∠2+∠3=180°,
∴AB∥CD (______________________).
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 . 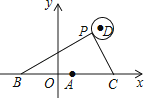
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题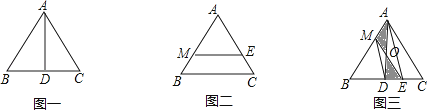
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
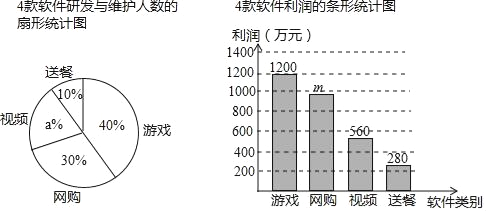
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 ![]() =
= ![]() .
. 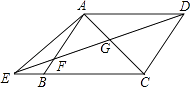
(1)求证:AB∥CD;
(2)如果AD2=DGDE,求证: ![]() =
= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数![]() 的图像经过点A(-1,1),下列各点中在该函数图象上的是( )
的图像经过点A(-1,1),下列各点中在该函数图象上的是( )
A. (1,5) B. (2,5) C. (-2,-2) D. (0,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.
(1)猜想AC与DE的数量关系,并说明理由。
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若![]() ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。
(3)设![]() ,
,![]() ,
,![]() 的面积分别是
的面积分别是![]() ,若
,若![]() ,试探究
,试探究![]() 与
与![]() 之间满足的等量关系。
之间满足的等量关系。
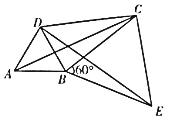
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,|4―(―2)|表示4与-2的差的绝对值,实际上也可以理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x―3|也可以理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空。
(1)求|8―(―3)|= ;|-3―5|= 。
(2)如图,x是0到4之间(包括0,4)的一个数,那么|x―1|+|x―2|+|x―3|+|x―4|的最小值等于多少?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com