
【题目】同学们都知道,|4―(―2)|表示4与-2的差的绝对值,实际上也可以理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x―3|也可以理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空。
(1)求|8―(―3)|= ;|-3―5|= 。
(2)如图,x是0到4之间(包括0,4)的一个数,那么|x―1|+|x―2|+|x―3|+|x―4|的最小值等于多少?
![]()
【答案】(1)11,8;(2)4
【解析】
(1)可先算出8与-3的差,(-3)与(-5)的和,然后再求出差的绝对值即可;
(2)根据绝对值的性质去掉绝对值号,然后计算即可得解.
解:
(1)|8―(―3)|=|8+3|=11,|-3―5|=|-8|=8.
故答案为:11;8;
(2)解:根据|x―1|+|x―2|+|x―3|+|x―4|的几何意义,可得|x―1|+|x―2|+|x―3|+|x―4|表示x到数轴上1,2,3,4四个数的距离之和。当x在2和3之间(即2<x<3)的任意位置时,x到数轴上1,2,3,4四个数的距离之和最小。
此时|x―1|+|x―2|+|x―3|+|x―4|=x―1+x―2+3―x+4―x=4。
所以|x―1|+|x―2|+|x―3|+|x―4|的最小值是4。
故答案为:4.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
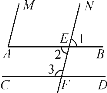
【题目】在括号里填入理由:如图,
∵∠A=75°,∠1=75°(已知),
∴∠A=∠1 (___________________),
∴AM∥EN (______________________).
又∵∠2=∠1(对顶角相等),
∠3=105°(已知),
∴∠2+∠3=180°,
∴AB∥CD (______________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,BC=AC,∠BCA=90°,P 为直线 AC 上一点,过 A作 AD⊥BP 于 D,交直线 BC 于 Q.
(1)如图 1,当 P 在线段 AC 上时,求证:BP=AQ.
(2)当 P 在线段 AC 的延长线上时,请在图 2 中画出图形,并求∠CPQ.
(3)如图 3,当 P 在线段 AC 的延长线上时,∠DBA= 时,AQ=2BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市12000名初中学生的视力情况,该校数学兴趣小组从该市七、八、九年级各随机抽取了100名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图. 
(1)由统计图可以看出年级越高视力不良率越(填“高”或“低”);
(2)抽取的八年级学生中,视力不良的学生有名;
(3)请你根据抽样调查的结果,估计该市12000名初中学生中视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
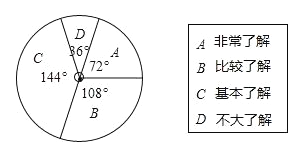
(1)求“非常了解”的人数的百分比.
(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球.
某校羽毛球队需要购买![]() 副球拍和
副球拍和![]() 盒羽毛球
盒羽毛球![]() .
.
(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含![]() 的代数式表示;
的代数式表示;
(2)当![]() 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
(3)当![]() 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( ) 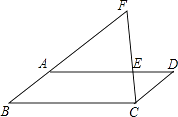
A.EF=2CE
B.S△AEF= ![]() S△BCF
S△BCF
C.BF=3CD
D.BC= ![]() AE
AE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com