
����Ŀ���ס��������̵����ͬ�����Ӻ�����ë���ĺ���ë��ÿ�����Ķ���300Ԫ��ÿ����ë��40Ԫ��Ϊ��ף��һ�ڣ������̵꿪չ��������£�
���̵꣺������Ʒ9���Żݣ�
���̵꣺ÿ��1����������1����ë��.
ijУ��ë�����Ҫ����![]() �����ĺ�
�����ĺ�![]() ����ë��
�����![]() .
.
(1)�������Ĵ�����ʽ����У��ë����ڼס��������̵��Ӧ���Ѷ���Ԫ�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
(2)��![]() ʱ�����жϷֱס��������̵깺�����ĺ���ë���ļұ��ˣ�
ʱ�����жϷֱס��������̵깺�����ĺ���ë���ļұ��ˣ�
(3)��![]() ����ʲô��ϵʱ�����ס��������̵깺�����ĺ���ë��ķ�����ͬ?
����ʲô��ϵʱ�����ס��������̵깺�����ĺ���ë��ķ�����ͬ?
���𰸡���1���ڼ��̵깺��ķ���Ϊ��270a+36b��Ԫ�������̵깺��ķ���Ϊ��260a+40b��Ԫ����2�������̵깺�����ĺ���ë����ˣ���3����a��b����5a=2b��ϵʱ�����ס��������̵깺�����ĺ���ë��ķ�����ͬ��
��������
��1��������������ô���ʽ�ֱ��ʾ��У��ë����ڼס��������̵��Ӧ���ѵ�Ǯ����
��2�����ݣ�1���д���ʽ����a=10��b=20���뼴�ɽ���⣻
��3������������Եõ���Ӧ�ĵ�ʽ���Ӷ����Եõ�a��b����ʲô�������ס��������̵깺�����ĺ���ë��ķ�����ͬ��
��1��������ɵã�
�ڼ��̵깺��ķ���Ϊ����300a+40b����0.9=��270a+36b����Ԫ����
�����̵깺��ķ���Ϊ��300a+40��b-a��=��260a+40b����Ԫ����
��2����a=10��b=20ʱ��
�ڼ��̵깺��ķ���Ϊ��270��10+36��20=3420��Ԫ����
�����̵깺��ķ���Ϊ��260��10+40��20=3400��Ԫ����
��3420>3400��
�൱a=10��b=25ʱ�������̵깺�����ĺ���ë����ˣ�
��3��������ɵã�
��270a+36b��-��260a+40b��=0��
��ã�5a=2b��
�𣺵�a��b����5a=2b��ϵʱ�����ס��������̵깺�����ĺ���ë��ķ�����ͬ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
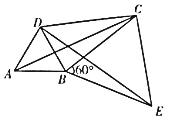
����Ŀ����ͼ��![]() ��
��![]() ���ǵȱ������Σ�����AC��DE��CD.
���ǵȱ������Σ�����AC��DE��CD.
��1������AC��DE��������ϵ����˵�����ɡ�
��2���������壺��һ���ı����д���һ���ڱߵ�ƽ������һ���Խ��ߵ�ƽ����������ı���Ϊ�����ı���.��ͼ����![]() ����֤���ı���ABCD�ǹ����ı��Ρ�
����֤���ı���ABCD�ǹ����ı��Ρ�
��3����![]() ��
��![]() ��
��![]() ������ֱ���
������ֱ���![]() ����
����![]() ����̽��
����̽��![]() ��
��![]() ֮������ĵ�����ϵ��
֮������ĵ�����ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�Ƕ�֪������4�D(�D2)����ʾ4�룭2�IJ�ľ���ֵ��ʵ����Ҳ��������Ϊ4�룭2����������������Ӧ������֮��ľ��룻ͬ����x�D3��Ҳ��������Ϊx��3����������������Ӧ������֮��ľ��룬��̽���������ա�
��1�����8�D(�D3)���� ������3�D5���� ��
��2����ͼ��x��0��4֮�䣨����0��4����һ��������ô|x�D1|��|x�D2|��|x�D3|��|x�D4|����Сֵ���ڶ��٣�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶ѧ����450�ˣ���������250�ˣ�Ů��200�ˣ���У�Ծ��꼶����ѧ��������һ���������ԣ��������ȡ��50��������40��Ů���IJ��Գɼ���Ϊ�������з��������Ƴ����µ�ͳ�Ʊ���
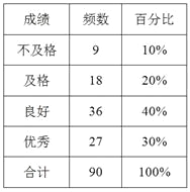
(1)����͡������ȡ��50��������40��Ů�����ĺ����ԣ�
(2)���ϱ��ġ�Ƶ���������ٷֱȡ�����������ѡ��һ�У����ʵ���ͳ��ͼ��ʾ��
(3)���Ƹ�У���꼶ѧ���������Գɼ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
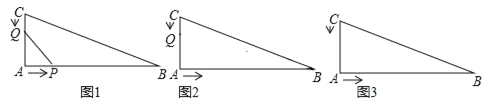
����Ŀ����ֱ��������ABC������AB=16cm��AC=12cm��BC=20cm����P�ӵ�A��ʼ��2����/����ٶ���A��B��C�ķ����ƶ�����Q�ӵ�C��ʼ��1����/����ٶ���C��A��B�ķ����ƶ��������P��Qͬʱ��������t���룩��ʾ�ƶ�ʱ������ô��
��1����ͼ1�����ú�t�Ĵ���ʽ��ʾ��������Q��AC��ʱ��CQ= ��������Q��AB��ʱ��AQ= ��
������P��AB��ʱ��BP= ��������P��BC��ʱ��BP= ��
��2����ͼ2������P���߶�AB���˶�����Q���߶�CA���˶�����QA=APʱ�������t��ֵ��
��3����ͼ3����P�㵽��C��ʱ��P��Q���㶼ֹͣ�˶�����AQ=BPʱ�������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y= ![]() x��˫����y=
x��˫����y= ![]() �Ľ���A�ĺ�����Ϊ2
�Ľ���A�ĺ�����Ϊ2
��1����k��ֵ
��2����ͼ������P��m��3����m��0����x��Ĵ��߽�˫����y= ![]() ��x��0���ڵ�M����ֱ��OA�ڵ�N
��x��0���ڵ�M����ֱ��OA�ڵ�N 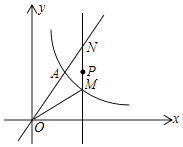
������OM����OA=OMʱ��ֱ��д��PN��PM��ֵ
���ԱȽ�PM��PN�Ĵ�С����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ��
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�50ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������3��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ��У���������ֽ���١��ڵı����Ƿ�ƽ�У�С����С���������ֲ�ͬ�ķ�����С����ֽ������AB�۵������á�1=��2=50�㣻С����ֽ������GH�۵�������GD��GC�غϣ�HF��HE�غϣ� �������ж���ȷ���ǣ� ��
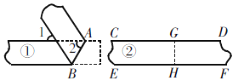
A. ֽ���ٵı���ƽ�У�ֽ���ڵı��߲�ƽ�� B. ֽ���١��ڵı��߶�ƽ��
C. ֽ���ٵı��߲�ƽ�У�ֽ���ڵı���ƽ�� D. ֽ���١��ڵı��߶���ƽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com