
����Ŀ��Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ�ǡ�MON����MON=135�㣩������Ϊ�ߣ����ܳ�Ϊ120m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ������ı���OBDGΪֱ�����Σ�
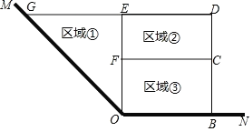
��1�����٢ڢ��������������ȣ���OB�ij�Ϊ m��
��2����OB=xm���ı���OBDG�����Ϊym2��
����y��x֮�ĺ�����ϵʽ����ע���Ա���x��ȡֵ��Χ����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
���𰸡���1��24����2����![]() ����0��x��60�����ڵ�x=15ʱ��y�����ֵ�����ֵΪ900.
����0��x��60�����ڵ�x=15ʱ��y�����ֵ�����ֵΪ900.
��������
��1������֤��EG=EO=DB��DE=FC=OB����OB=CF=DE=x����![]() ���ɢ٢ڢ��������������ȣ��õ�
���ɢ٢ڢ��������������ȣ��õ�![]() ���ⷽ�̼��ɣ�
���ⷽ�̼��ɣ�
��2���ٸ���ֱ�����ε������ʽ���㼴�ɣ������ö��κ������������y�����ֵ���Լ���ʱx��ֵ���ɣ�
�⣺��1���⣺��1���������֪����MON=135������EOB=��D=��DBO=90����
���EGO=��EOG=45����
��EG=EO=DB��DE=FC=OB����OB=CF=DE=x����![]() ��
��
�ߢ٢ڢ��������������ȣ�
 ��
��
��x=24��60����������
��BC=24m��
�ʴ�Ϊ24��
��2���������֪����MON=135������EOB=��D=��DBO=90����
���EGO=��EOG=45����
��CF=DE=OB=x����GE=OE=BD=![]() (120-2x)=40-
(120-2x)=40-![]() x
x
��y=
= ![]() ��0��x��60��
��0��x��60��
��![]()
=![]()
�൱x=15ʱ��y�����ֵ�����ֵΪ900.



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
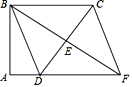
����Ŀ����ͼ1���ڡ�ABC�У�AB��BC��5��AC��6����ECD�ǡ�ABC��BC����ƽ�Ƶõ��ģ�����AE��AC��BE�ཻ�ڵ�O��
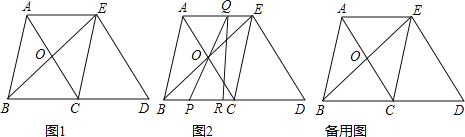
��1���ж��ı���ABCE���������ı��Σ�˵�����ɣ�
��2����ͼ2��P���߶�BC��һ���㣨ͼ2�����������B��C�غϣ�������PO���ӳ����߶�AE�ڵ�Q��QR��BD������Ϊ��R��
���ı���PQED������Ƿ����P���˶��������仯�����仯����˵�����ɣ������䣬����ı���PQED�������
�ڵ��߶�PB�ij�Ϊ��ֵʱ����PQR���BOC���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��Ϊ��O�����ߣ��е�ֱ�ΪB��C����D���Ż�BC��һ�㣬�����й�ϵʽ�У�һ���������ǣ�������
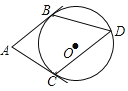
A. ��A+��D��180��B. ��A+2��D��180��
C. ��B+��C��270��D. ��B+2��C��270��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y����x2+bx+c��һֱ���ཻ��A��1��0����C����2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1����������ֱ��AC�ĺ�����ϵʽ��
��2����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ����ʱ��P�����ꣻ
��3���ڶԳ������Ƿ����һ��M��ʹ��ANM���ܳ���С�������ڣ������M����������ANM�ܳ�����Сֵ���������ڣ���˵�����ɣ�
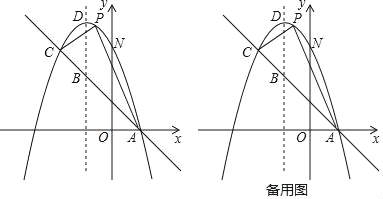
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A=��ABC=90�㣬AD=2��BC=6����E�DZ�CD���е㣬����BE���ӳ���AD���ӳ����ڵ�F������CF������BCD�ǵ��������Σ����ı���BDFC�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�ضԽ���BD�۵���ʹ��A����ƽ���ϵ�F�㴦��DF��BC�ڵ�E��
��1����֤����DCE�ա�BFE��
��2����CD=2����ADB=30������BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��EΪ����ABCD�ı�AD��һ�㣬��P�ӵ�B����������BE-ED-DC�˶�����Cֹͣ����Q�ӵ�B������BC�˶�����Cֹͣ�������˶����ٶȶ���1cm/s������P����Qͬʱ��ʼ�˶������˶�ʱ��Ϊt��s������BPQ�����Ϊy��![]() ������֪y��t֮��ĺ���ͼ����ͼ2��ʾ��
������֪y��t֮��ĺ���ͼ����ͼ2��ʾ��

�������н��ۣ��ٵ�0��t��10ʱ����BPQ�ǵ��������Σ���![]() =48
=48![]() ���۵�14��t��22ʱ��y=110-5t�������˶������У�ʹ�á�ABP�ǵ��������ε�P��һ����3�����ݡ�BPQ���ABE����ʱ��t=14.5��
���۵�14��t��22ʱ��y=110-5t�������˶������У�ʹ�á�ABP�ǵ��������ε�P��һ����3�����ݡ�BPQ���ABE����ʱ��t=14.5��
������ȷ���۵������_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�죬ˮ����Ӫ��������1600Ԫ��ˮ�������г�����⨺��Һ�â����50ǧ�ˣ����ٵ�ˮ���г�ȥ������֪⨺��Һ�â������������ۺ����ۼ������ʾ��
Ʒ�� | ⨺��� | â�� |
������ | 20 | 40 |
���ۼ� | 26 | 50 |
![]() ��������⨺��Һ�â��������ǧ�ˣ�
��������⨺��Һ�â��������ǧ�ˣ�
![]() ���⨺��Һ�â��ȫ�����꣬��������Ǯ��
���⨺��Һ�â��ȫ�����꣬��������Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ѧ����Ϊ���㾭֮�����ġ��������������й��Ŵ��㷨�Ŀ���֮�����������������м��أ���������ȸ�����࣬����֮�⣬ȸ���أ�����ᣮһȸһ�ཻ����������ƽ�����ࡢȸ��һ����ࡢȸһö���ؼ��Σ���
���ģ�������![]() ֻȸ��
ֻȸ��![]() ֻ�࣬�ֱ�۽������ú�����֮������һ���ȸ�أ����ᣮ��һֻȸ��һֻ�ཻ��λ�ö��ţ�������ȣ�
ֻ�࣬�ֱ�۽������ú�����֮������һ���ȸ�أ����ᣮ��һֻȸ��һֻ�ཻ��λ�ö��ţ�������ȣ�![]() ֻȸ��
ֻȸ��![]() ֻ������Ϊ
ֻ������Ϊ![]() ���ȸ����ÿ
���ȸ����ÿ![]() ֻ���ض��ٽ��
ֻ���ض��ٽ��
���з���������������⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com