
已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2,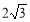 ).
).

(1)请判断 的形状并说明理由.
的形状并说明理由.
(2)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥ 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值
(1)△POA是等边三角形;
(2)①当0<t≤4时,S=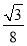
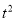 ,当4<t<8时,S=-
,当4<t<8时,S=-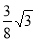
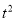 +4
+4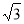 t-8
t-8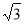 ;②当t=
;②当t=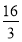 时,S最大=
时,S最大=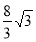 .
.
【解析】
试题分析:(1)由两直线相交可列出方程组,求出P点坐标;
(2)将y=0代入y=﹣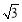 x+4
x+4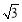 ,可求出OA=4,作PD⊥OA于D,则OD=2,PD=2
,可求出OA=4,作PD⊥OA于D,则OD=2,PD=2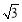 ,利用tan∠POA=
,利用tan∠POA=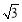 ,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
(3)①当0<t≤4时,在Rt△EOF中,∠EOF=60°,OE=t,可以求出EF,OF,从而得到S;
②分情况讨论当0<t≤4时,t=4时,当4<t<8时,S的值,最终求出最大值.
试题解析:
△POA是等边三角形.理由:
将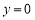 代入
代入
 ,
,
∴ 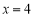 ,即OA=4
,即OA=4
作PD⊥OA于D,则OD=2,PD=2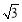 ,
,
∵ tan∠POA=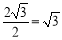 ,
,
∴ ∠POA=60°,
∵ OP=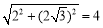
∴△POA是等边三角形 ;
(2)① 当0<t≤4时,如图1

在Rt△EOF中,
∵∠EOF=60°,OE=t
∴EF=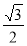 t,OF=
t,OF=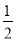 t
t
∴S=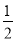 ·OF·EF=
·OF·EF=
当4<t<8时,如图2

设EB与OP相交于点C,
易知:CE=PE=t-4,AE=8-t,
∴AF=4-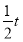 ,EF=
,EF=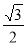 (8-t),
(8-t),
∴OF=OA-AF=4-(4-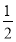 t)=
t)=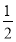 t,
t,
∴S=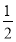 (CE+OF)·EF,
(CE+OF)·EF,
=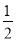 (t-4+
(t-4+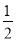 t)×
t)×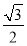 (8-t),
(8-t),
=-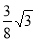
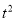 +4
+4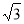 t-8
t-8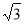 ;
;
② 当0<t≤4时,S=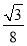
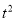 , t=4时,S最大=2
, t=4时,S最大=2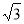
当4<t<8时,S=-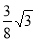
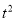 +4
+4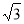 t-8
t-8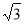 =-
=-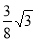 (t-
(t-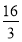 )
)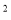 +
+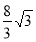
t=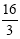 时,S最大=
时,S最大=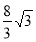
∵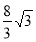 >2
>2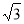 ,
,
∴当t=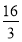 时,S最大=
时,S最大=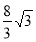 .
.
考点:一次函数综合题.


科目:初中数学 来源:2013-2014学年广东省九年级下册期末检测数学试卷(解析版) 题型:解答题
如图,已知Rt△ABC中,∠C=90°,CB=8,CA=6.
(1)求作⊙O,使⊙O过点C,圆心O在CB上,且与边AB相切(用尺规作图,不写作法,保留痕迹)
(2)求⊙O的半径

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省云浮市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,P是等边△ABC内的一点,若将△PAB绕点A逆时针旋转得到△P’AC,则∠PAP’的度数为

A.120° B.90° C.60° D.30°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省中考预测二数学试卷(解析版) 题型:填空题
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,若AC=4,则四边形CODE的周长为

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省中考预测二数学试卷(解析版) 题型:选择题
下列计算正确的是( )
A.a3•a4=a12 B.(a3)4=a7
C.(a2b)3=a6b3 D.a3÷a4=a(a≠0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东汕头市九年级下学期第一次阶段考试数学试卷(解析版) 题型:解答题
如图,有两个可以自由转动的均匀转盘 ,都被分成3等份,每份内均标有数字,小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘
,都被分成3等份,每份内均标有数字,小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘 和
和 ,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.
,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.

(1)请画出树状图,求小明获胜的概率 和小亮获胜的概率
和小亮获胜的概率 .(直接写出答案不给分)
.(直接写出答案不给分)
(2)通过(1)的计算结果说明该游戏的公平性.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东青岛平度古岘镇古岘中学九年级下学期阶段性质量检测数学试卷(解析版) 题型:解答题
益家果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千 克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利 还是亏损?盈利或亏损了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com