
【题目】周末,甲从家出发前往与家相距![]() 千米的旅游景点旅游,以
千米的旅游景点旅游,以![]() 千米/时的速度步行
千米/时的速度步行![]() 小时后,改骑自行车以
小时后,改骑自行车以![]() 千米/时的速度继续向目的地出发,乙在甲前面
千米/时的速度继续向目的地出发,乙在甲前面![]() 千米处,在甲出发
千米处,在甲出发![]() 小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离
小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离![]() (千米)与甲出发的时间
(千米)与甲出发的时间![]() (小时)之间的函数关系如图所示.
(小时)之间的函数关系如图所示.
(1)求乙的速度;
(2)求甲出发多长时间后两人第一次相遇;
(3)求甲出发几小时后两人相距![]() 千米. .
千米. .

【答案】(1)乙的速度为![]() 千米/时;(2)甲出发
千米/时;(2)甲出发![]() 小时后两人第一次相遇;(3)甲出发
小时后两人第一次相遇;(3)甲出发![]() 小时或
小时或![]() 小时或
小时或![]() 小时后两人相距
小时后两人相距![]() 千米
千米
【解析】
(1)先求出甲走完全程的时间就可求出乙走完全程的时间,由速度等于路程除以时间即可解题,(2)设直线AB的解析式为y=kx+b,利用待定系数法即可解题,(3)分类讨论即可
解: (1)甲行驶完全程的时间为:![]() 小时.
小时.
乙的速度为:![]() 千米/时.
千米/时.
答:乙的速度为![]() 千米/时;
千米/时;
(2)设直线![]() 的解析式为y=kx+b:由题意,得
的解析式为y=kx+b:由题意,得
![]()
解得: ![]()
![]()
当![]() 时,
时,
![]() ,得
,得![]() .
.
答:甲出发![]() 小时后两人第一次相遇;
小时后两人第一次相遇;
(3)当乙不动时,
当![]() 时,
时,
解得:![]() .
.
当![]() 时
时
解得:![]() .
.
当甲乙均在运动时,设运动的时间为![]() ,
,
则 ![]() (
(![]() 为乙的速度),
为乙的速度),
解得![]() .
.
答:甲出发![]() 小时或
小时或![]() 小时或
小时或![]() 小时后两人相距
小时后两人相距![]() 千米.
千米.


科目:初中数学 来源: 题型:
【题目】已知四边形ABCD∽四边形A′B′C′D′,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用函数方法研究动点到定点的距离问题.
在研究一个动点P(x,0)到定点A(1,0)的距离S时,小明发现:
S与x的函数关系为S= 并画出图像如图:
并画出图像如图:

借助小明的研究经验,解决下列问题:
(1)写出动点P(x,0)到定点B(-2,0)的距离S的函数表达式,并求当x取何值时,S取最小值?
(2)设动点P(x,0)到两个定点M(1,0)、N(5,0)的距离和为y.
①随着x增大,y怎样变化?
②当x取何值时,y取最小值,y的最小值是多少?
③当x<1时,证明y随着x增大而变化的规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点
的图象经过点![]() 则
则
(1)求这个函数表达式;
(2)画出该函数的图像;
(3)写出把这条直线向下平移![]() 个单位长度后的函数关系式是
个单位长度后的函数关系式是
(4)求平移后的图像与两条坐标轴围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
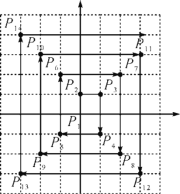
【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),…,根据这个规律,点P2 019的坐标为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副扑克牌中取出方块3、红心6、黑桃10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字,这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同时,则视为平局.
(1)用画树状图或列表法,表示出小明、小丽两人一次游戏的所有可能的结果;
(2)求小明获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com