

���� ��1������ֱ��l2����ʽ���B��D���꣬������ֱ�߽���ʽ���A���ꣻ
��2��ȷ����OB��OD�ij������ù��ɶ������BD�ij������������ʽ���OC�ij�������C��ֱ��l2�ϣ����C���꣬���ݹ��ɶ������x��ֵ��ȷ����C���꣬��C��CF��OB�ڵ�F����P��PE��OB�ڵ�E�����CF��OF�ij�����OP=t����PE��CFƽ�У��ó�������POE��������COF���ƣ������Ƶñ�������ʾ��PE��OE�ij����ó�P���꣬������ʾ��M���꣬��������ľ��빫ʽ��ʾ��AM��t�Ĺ�ϵʽ����ΪS��t�Ĺ�ϵʽ�������t�ķ�Χ���ɣ�
��3���ڵ�P���˶������У�AM���ܵ���AB������Ϊ���ɱ�ʾ����AM��AB��ȣ����������ľ��빫ʽ�г�����t�ķ��̣����t��ֵ�����鼴�������жϣ�
��� �⣺��1�������ã�$\left\{\begin{array}{l}{y=4x}\\{y=-\frac{4}{3}x+\frac{20}{3}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{5}{4}}\\{y=5}\end{array}\right.$����A��$\frac{5}{4}$��5����
��2����OD=$\frac{20}{3}$��OB=5��
����ݹ��ɶ����ã�BD=$\sqrt{O{D}^{2}+O{B}^{2}}$=$\frac{25}{3}$��
��S��BOD=$\frac{1}{2}$OD•OB=$\frac{1}{2}$BD•OC���õ�OC=$\frac{OB•OD}{BD}$=$\frac{5��\frac{20}{3}}{\frac{25}{3}}$=4��
�ߵ�C��y=-$\frac{4}{3}$x+$\frac{20}{3}$�ϣ���C��x��-$\frac{4}{3}$x+$\frac{20}{3}$����
��Rt��COF�У����ݹ��ɶ����ã�OC2=OF2+CF2����x2+��-$\frac{4}{3}$x+$\frac{20}{3}$��2=42��
��ã�x=$\frac{16}{5}$��
��C��$\frac{16}{5}$��$\frac{12}{5}$����
��C��CF��OB�ڵ�F����P��PE��OB�ڵ�E������CF=$\frac{12}{5}$��OF=$\frac{16}{5}$��
��OP=t��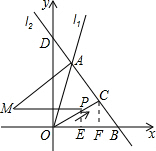
��PE��CF��
���POE�ס�COF��
��$\frac{PE}{CF}$=$\frac{OE}{OF}$=$\frac{OP}{OC}$����$\frac{PE}{\frac{12}{5}}$=$\frac{OE}{\frac{16}{5}}$=$\frac{t}{4}$��
��ã�PE=$\frac{3}{5}$t��OE=$\frac{4}{5}$t����P��$\frac{4}{5}$t��$\frac{3}{5}$t����
��M��-$\frac{4}{5}$t��$\frac{3}{5}$t����
��AM2=[$\frac{5}{4}$-��-$\frac{4}{5}$t��]2+��5-$\frac{3}{5}$t��2��
��������ã�S=AM=$\sqrt{[\frac{5}{4}-��-\frac{4}{5}t��]^{2}+��5-\frac{3}{5}t��^{2}}$=$\sqrt{{t}^{2}-4t+\frac{425}{16}}$��0��t��4����
��3���ڵ�P���˶������У�AM���ܵ���AB������Ϊ��
��l2��y=-$\frac{4}{3}$x+$\frac{20}{3}$��y�ύ�ڵ�D����D��0��$\frac{20}{3}$������x�ύ�ڵ�B��5��0����
��OD=$\frac{20}{3}$��OB=5��
��M��-$\frac{4}{5}$t��$\frac{3}{5}$t����ҪʹAM=AB������[$\frac{5}{4}$-��-$\frac{4}{5}$t��]2+��5-$\frac{3}{5}$t��2=��5-0��2+��5-$\frac{5}{4}$��2��
��ã�t=2��$\frac{\sqrt{66}}{2}$���������⣬
���ڵ�P���˶������У�AM���ܵ���AB��
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У���ֱ�ߵĽ������꣬���ɶ����������������ʽ��������ͼ�����ʣ����������ε��ж������ʣ��Լ������ľ��빫ʽ���������չ�ʽ�������ǽⱾ��Ĺؼ���


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.5��10-5 | B�� | 0.25��10-7 | C�� | 2.5��10-6 | D�� | 25��10-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a•a2=a2 | B�� | a2��a=2 | C�� | 2a2+a2=3a4 | D�� | ��-a��3=-a3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ĸ�����ȵ��ı����Ǿ��� | B�� | �Խ��ߴ�ֱ���ı��������� | ||
| C�� | �Խ�����ȵ��ı����Ǿ��� | D�� | �ı���ȵ��ı����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
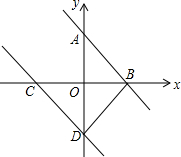 ��ͼ����֪һ��ֱ�߾�����A��0��3������B��2��0����������ֱ������ƽ����x�ᡢy��ֱ��ڵ�C����D����DB=DC����ֱ��CD�ĺ�������ʽ��
��ͼ����֪һ��ֱ�߾�����A��0��3������B��2��0����������ֱ������ƽ����x�ᡢy��ֱ��ڵ�C����D����DB=DC����ֱ��CD�ĺ�������ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
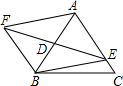 ��ͼ���ڵȱߡ�ABC�У�AB=1��DΪAB�ߵ��е㣬EΪֱ��AC��һ�㣬����ED���ӳ�����ED���ӳ�����ȡ��F��ʹDF=DE������AF��BF��BE��
��ͼ���ڵȱߡ�ABC�У�AB=1��DΪAB�ߵ��е㣬EΪֱ��AC��һ�㣬����ED���ӳ�����ED���ӳ�����ȡ��F��ʹDF=DE������AF��BF��BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
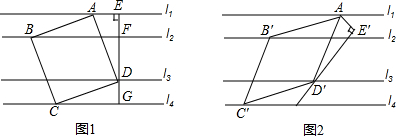
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com